Информационные свойства фазовых спектров сейсмических сигналов
Иванченков В.П., Кочегуров А.И., Орлов О.В.

Аннотация

В статье рассматриваются возможности использования информационных параметров фазочастотных характеристик отраженных сейсмических волн для решения структурных задач и прогноза свойств геологического разреза. Приводятся результаты разработки и исследования ряда фазочастотных методов анализа сложных волновых полей. Показывается высокая эффективность фазочастотных методов, приводятся примеры их применения для обработки данных.

Ключевые слова: фазовые спектры, сейсмические сигналы, информационные параметры, фазочастотные методы, сложные волновые поля.

На всех этапах обработки и интерпретации сейсмических материалов, получаемых при поиске и разведке нефтяных и газовых месторождений, широко используются различные спектрально-аналитические методы, в которых в качестве информативных параметров применяются преимущественно амплитудные и энергетические спектры отраженных сейсмических волн [1–3]. В значительно меньшей степени используются фазочастотные характеристики (ФЧХ) сейсмических сигналов. Между тем в фазовые спектры сейсмических сигналов заложена важная информация о структурных, скоростных, поглощающих и дисперсионных свойствах геологического разреза [4–6]. На этой основе могут быть синтезированы фазочастотные алгоритмы, позволяющие в условиях априорной неопределенности относительно формы исследуемых волн обнаруживать и разрешать сигналы на фоне интенсивных помех и получать надежные оценки их параметров [7]. Использование ФЧХ отражений оказывается также полезным при решении задач прогноза геологического разреза, в том числе прогноза нефтегазоносности осадочных толщ [8].

В данной работе кратко излагаются результаты исследований информационных параметров фазовых характеристик отраженных волн, разработки на их основе ряда фазочастотных методов решения отдельных задач прогноза геологического разреза, а также приводятся примеры применения предложенных методов, подтверждающие их эффективность.

Рассмотрим свойства ФЧХ сейсмических сигналов, предварительно обратив внимание на эффект стационарности фазовых спектров отраженных волн. Проведенные исследования на наиболее часто используемых моделях сейсмических импульсов (импульс Берлаге, импульс с колокольной огибающей и др.) показали, что при определенной протяженности окна анализа и совмещения его центра с максимумами сигналов их фазовые спектры в основной полосе частот принимают постоянное, не зависящее от частоты значение (область стационарной фазы) [9].

Рис. 1. Эффект стационарности фазового спектра импульса Берлаге

а — импульс Берлаге; б — фазовый спектр в широком окне анализа; в — фазовый спектр в узком окне анализа

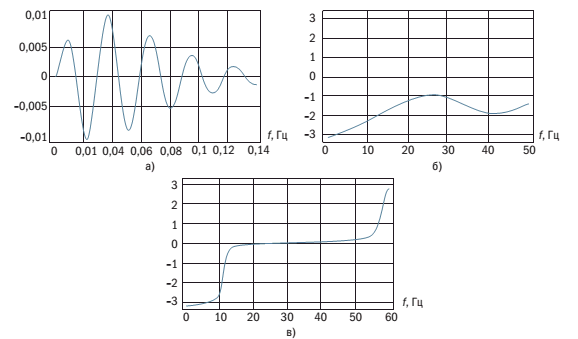
На рисунке 1а в качестве примера показан импульс Берлаге:

Здесь , n – параметры, определяющие конкретный вид огибающей импульса, - преобладающая частота. ФЧХ импульса Берлаге (n=1, 2) не является постоянной ни при каких параметрах и n (рис. 1б). Однако если ограничить длительность импульса, выбрав окно анализа, равное 2–3 видимым периодам, а нулевую точку отсчета времени расположить в центре окна анализа, то фазовый спектр в определенной полосе частот становится практически стационарным (рис. 1в).

Проведенные исследования показали, что в общем случае границы области стационарной фазы при ограничении длительности сейсмоимпульсов с достаточной точностью определяются полосой частот:

,

где T – длительность окна анализа.

Установленное условие стационарности ФЧХ сейсмоимпульсов нашло подтверждение при изучении спектров отраженных волн, полученных при сейсмических исследованиях в ряде районов Западной Сибири [8]. Использование информации о стационарности ФЧХ сейсмических сигналов позволило синтезировать ряд фазочастотных алгоритмов прослеживания волн и построить на их основе объектно-ориентированные фазовые разрезы, нашедшие применение при построении целевых отражающих горизонтов.

Важной задачей при прогнозе геологического разреза являются выявление и изучение взаимосвязей фазовых спектров отраженных волн и петрофизических параметров анализируемых геологических сред. С этой целью были проведены исследования информационных свойств фазовых спектров волн на ряде моделей слоистых поглощающих сред. При этом использовался один из широко распространенных подходов, когда среда рассматривается в виде линейной системы, вносящей определенные изменения в проходящие через нее колебания [1, 2]. Суть применяемого системного подхода можно проиллюстрировать на примере простой модели слоистой поглощающей толщи (рис. 2а). При нормальном падении волны S(t) в лучевом приближении процесс отражения от кровли и подошвы линейно неупругого слоя II можно представить в виде эквивалентной системы, показанной на рисунке 2б.

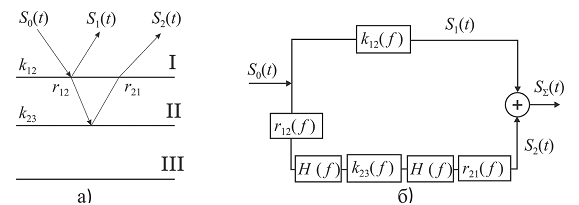
Рис. 2. Модель плоскопараллельной слоистой поглощающей толщи

Комплексные спектры волн, отраженных от кровли и подошвы II слоя, могут быть соответственно представлены:

,

,

где и – коэффициенты отражения от кровли и подошвы II слоя; и – коэффициенты преломления на кровле II слоя; QUOTE – частотная характеристика системы, характеризующая распространение волны в поглощающем слое II в двух направлениях; QUOTE – спектр падающей волны. Следует отметить, что коэффициенты отражения и преломления в поглощающих средах являются комплексными функциями.

Функция

(1)

определяет фазовый спектр отраженной волны , который непосредственно зависит от аргументов коэффициентов преломления и отражения , а также от ФЧХ системы , определяющей распространение волны в поглощающем слое и начальной фазы падающей волны .

В соответствии с [7, 8] аргументы коэффициентов отражения и преломления могут быть записаны в следующей форме:

,

, (2)

где – отношение акустических жесткостей в средах I и II; , – соответственно скорость распространения продольных волн и плотность среды; – декремент поглощения; – коэффициент поглощения в i-ой среде (i=1, 2).

Следующей составляющей фазового спектра волны, отраженной от подошвы второго слоя, является функция , определяющая фазовый набег при распространении волны в этом поглощающем слое. Принимая для поглощающего слоя минимально фазовую модель среды и допущение о линейной зависимости коэффициента поглощения от частоты согласно [1] выражение для модуля и аргумента можно привести к виду:

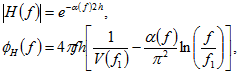(3)

где h – мощность II слоя; QUOTE – скорость распространения на некоторой базовой частоте .

Из (3) видно, что нелинейная составляющая определяется поглощающими свойствами анализируемого слоя. По аналогии может быть построена модель поглощающей среды, состоящей из произвольного числа слоев [8].

Таким образом, из выражений 1–3 видно, что петрофизические параметры исследуемой толщи оказывают непосредственное влияние на ФЧХ отраженных волн.

Исследование данного влияния проводилось на ряде моделей слоистых поглощающих сред. Четыре такие модели приведены на рисунке 3. Они характеризуются наличием слоя песчаника, расположенного во вмещающей толще аргиллита. В первой модели песчаный слой предполагался насыщенным газом, во второй – нефтью, в третьей – водой. В четвертой модели имитировалось наличие непроницаемого карбонизированного песчаника. Скорости продольных волн, плотности сред, акустические жесткости и декременты поглощения во всех слоях выбирались исходя из обобщенных данных, характерных для верхнеюрской продуктивной толщи Томского Приобья.

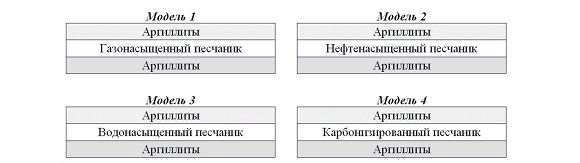
Рис. 3. Геологические модели слоистых поглощающих сред

На рисунке 4 изображены фазовые спектры отраженной волны от подошвы второго слоя, полученные для четырех рассматриваемых моделей сред. Данные характеристики были построены на основе оценки семейства аргументов коэффициентов отражения, вычисляемых при различных декрементах поглощения контактирующих слоев. Заштрихованные области на рисунках определяют пределы изменения фазовых спектров отраженных волн в зависимости от параметров поглощения второго слоя. Наибольшие изменения фазовых спектров отраженных волн, как видно из рисунка, наблюдаются для газонасыщенного коллектора (рис. 4а) и нефтенасыщенного песчаника (рис. 4б). В случае насыщения песчаного коллектора водой (рис. 4в) обобщенные фазовые спектры коэффициентов отражения слабо зависят от частоты, и их значения сосредоточены в промежуточной области 0 1 рад или -2 -3 рад. При отсутствии коллектора фазовые спектры изменяются незначительно и практически не зависят от частоты (рис. 4г). Их значения близки к 0 или π.

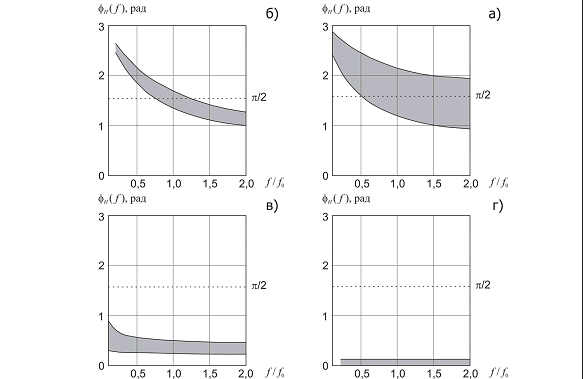
Рис. 4. Обобщенные фазовые спектры отражения волн от кровли второго слоя

Проведенные исследования на ряде других моделей слоистых поглощающих сред также показали, что фазовые спектры отраженных волн значимо зависят от изменения акустических и поглощающих свойств среды. Это может служить важной предпосылкой использования ФЧХ отраженных волн в качестве диагностических признаков при решении задач прогноза геологического разреза, в том числе прогноза нефтегазоносности осадочных толщ. На базе данных исследований и рассмотренного выше свойства стационарности ФЧХ отраженных волн разработаны фазочастотные алгоритмы их прослеживания.

Прослеживание сейсмических волн и границ занимает одно из ведущих положений при решении задач структурной сейсморазведки. Не меньшее значение имеет прослеживание волн при решении задач прогноза геологического разреза. На практике довольно часто приходится решать задачи прослеживания волн в условиях их интенсивной интерференции. Такая ситуация наиболее характерна при исследованиях тонкослоистых сред, где, как правило, приходится осуществлять прослеживание волн в условиях, когда форма сигналов неизвестна. В этой связи реализуемые алгоритмы прослеживания сейсмических волн должны обладать повышенной разрешающей способностью и позволять достаточно надежно осуществлять оценку их кинематических параметров в условиях неполной априорной информации о свойствах выделяемых сигналов.

Предварительно рассмотрим оптимальный метод прослеживания фиксированных сейсмических волн, наблюдаемых на фоне гауссовых помех, который реализуется в виде процедуры поиска максимума функции правдоподобия [5]:

. (4)

Здесь – отклонение фазового спектра сигнала от фазового спектра смеси сигнала и шума; – пиковое отношение сигнала к шуму на частоте .

Практическое применение оптимальных фазочастотных алгоритмов вида (4) наталкивается на ряд проблем, в частности связанных с оценкой распределения величин в исследуемом диапазоне частот. Действительно, форма регистрируемых сейсмических сигналов, как правило, неизвестна, следовательно неизвестны . При этом обычно неизвестно точное значение фазового спектра выделенных сигналов. В этой связи были предложены фазочастотные алгоритмы (ФЧП) прослеживания волн. Эти алгоритмы получены из оптимального метода путем замены в (4) весовой функции на другие, специально подобранные, функции. В общем случае функция качества (критерий оценки временного положения сигналов) для таких алгоритмов может быть записана в виде [6]:

, (5)

где – частотная весовая функция, вид которой зависит от реализуемого фазочастотного алгоритма; – мгновенный фазовый спектр участка трассы, вычисляемый в скользящем окне анализа.

Весовая функция может быть задана в треугольной, синусоидальной или экспоненциальной форме. Определение временного положения сигнала при этом осуществляется путем оценки местоположения экстремума функции качества (5).

На рисунке 5 приведена схема, поясняющая процедуру прослеживания волн в реализуемых алгоритмах. Вдоль выбранной сейсмической трассы перемещается окно анализа, для каждого положения которого определяется мгновенный фазовый спектр выделенного участка трассы и проводится вычисление функции качества (5). После прохождения требуемого интервала сейсмотрассы определяется положение экстремума функции качества и оценивается время прихода сигнала в данную точку приема.

Рис. 5. Схема, поясняющая процедуру фазочастотного прослеживания сейсмических волн

Исследование эффективности предложенных алгоритмов ФЧП проводилось на различных моделях волновых полей. Так, на рисунке 6 приведены результаты исследования помехоустойчивости алгоритмов ФЧП в условиях, когда прослеживание сигналов осуществлялось на фоне гауссовых нерегулярных помех. График иллюстрирует зависимость среднеквадратической погрешности оценки временного положения сигнала σ от пикового отношения сигнала к шуму δ. Видно, что даже при отношении сигнала к шуму, равному единице, погрешность оценки временного положения не превышает 6 мс, что свидетельствует о достаточно высокой помехоустойчивости алгоритмов ФЧП.

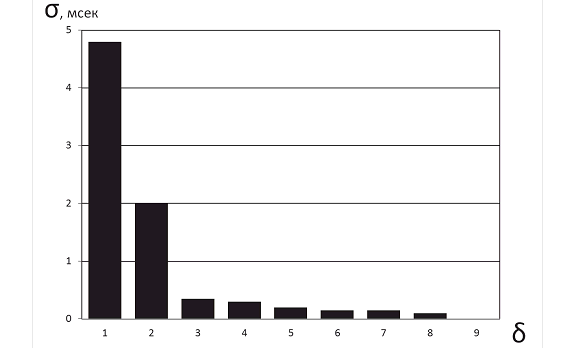
Рис. 6. Оценка помехоустойчивости алгоритмов ФЧП



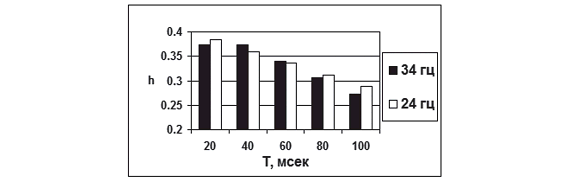
Рис. 7. Разрешающая способность алгоритма ФЧП для сигналов с частотой 24 и 34 Гц

Как уже отмечалось выше, при решении задач прослеживания и детального расчленения тонкослоистых продуктивных толщ особо важное значение приобретает обеспечение повышенного разрешения выделяемых сейсмических сигналов. На рисунке 7 в качестве примера показаны результаты исследования разрешающей способности методов ФЧП на моделях сейсмических волновых полей [10]. Здесь ; – длина волны сейсмического импульса; – расстояние между интерферируемыми импульсами; Т – длительность окна анализа. Как видно из рисунка, данный метод обеспечивает достаточно высокое разрешение, порядка трети длины волны.

На базе предложенных методов ФЧП, наряду с прослеживанием сейсмических волн, были реализованы алгоритмы построения объектно ориентированных разрезов и фазовременного (ФАН) анализа [11]. При построении объектно ориентированных разрезов функция качества алгоритмов прослеживания определяется для различных пикетов наблюдения и отображается во временном интервале, соответствующем анализируемым толщам. ФАН-анализ используется при прогнозе типов геологического разреза около- и межскважинного пространства [8]. Для каждой анализируемой сейсмотрассы в области исследуемой толщи формируется совокупность функций (5):

, (6)

где – специально подобранная весовая функция, частотные параметры которой целенаправленно изменяются в процессе ФАН-анализа.

Совокупность функций вида (6) образует ФАН-колонку (ФАН-образ) для данной сейсмотрассы, а их совокупность для набора сейсмотрасс вдоль профиля наблюдения образует ФАН-разрез.

Для решения этой задачи привлекаются данные геофизического исследования скважин и имеющиеся материалы по скважинам, пробуренным на исследуемой площади. На основе этих данных при проведении ФАН-анализа получают ФАН-образы для пикетов наблюдения, соответствующих положению скважин. Эти ФАН-образы используются в качестве эталонных при прогнозе типов геологического разреза в около- и межскважинном пространстве.

По данным ФАН строятся карты распространения типов разрезов для изучаемой площади. По результатам комплексной интерпретации структурных построений и всех материалов фазочастотной обработки формируются предложения по оценке продуктивности анализируемых толщ.

На базе предложенных фазочастотных методов была проведена обработка материалов сейсмических исследований ОГТ и ВСП, полученных в условиях Томской и Тюменской областей. Общий анализ представленных для обработки разрезов ОГТ показал, что наблюдаемые волновые поля для исследуемых толщ имеют, как правило, сложный интерференционный характер, отражающий тонкослоистый геологический разрез со сложным пространственным распределением слагающих его элементов. В ряде случаев отражения от анализируемых горизонтов динамически невыразительны, неустойчивы по латерали и прослеживаются спорадически. При детальной обработке временных разрезов ОГТ были построены объектно ориентированные разрезы на основе алгоритмов ФЧП, а также горизонтальные ФАН разрезы.

В целом проведенное по результатам обработки сопоставление временных разрезов ОГТ и объектно ориентированных фазовых разрезов показало, что применение ФЧП значительно улучшает разрешение волн в области их интенсивной интерференции, а также позволяет выделять и прослеживать слабые по интенсивности отражения. На рисунках 8−10 приведены отдельные результаты обработки материалов ОГТ с помощью предложенных фазочастотных алгоритмов.

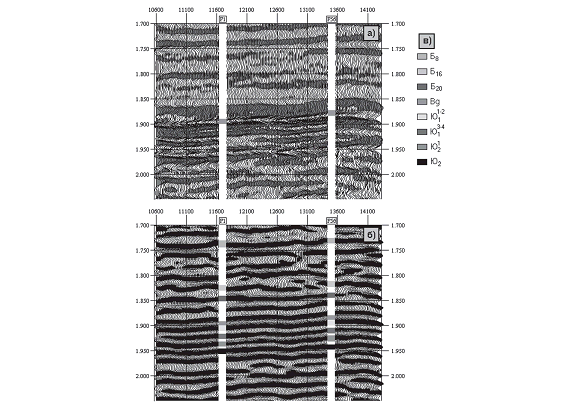
Рис. 8. Фрагменты временных разрезов ОГТ и ФЧП профиля Мыльджинского газоконденсатного месторождения:
а – фрагмент разреза ОГТ; б – фрагмент разреза ФЧП

Так, на рисунке 8 представлены фрагменты разреза ОГТ и полученного объектно ориентированного разреза (разреза ФЧП) для одного из профилей Мыльджинского газоконденсатного месторождения Томской области. Как видно из рисунка, на разрезе ФЧП, в отличие от разреза ОГТ, удается выделить и привязать все основные отражающие горизонты нижнего мела и верхней юры, причем уверенно прослеживаются даже очень слабые по интенсивности отражения. На разрезах ФЧП, по сравнению с разрезами ОГТ, более отчетливо проявляются различные неоднородности исследуемого геологического разреза (рис. 9).

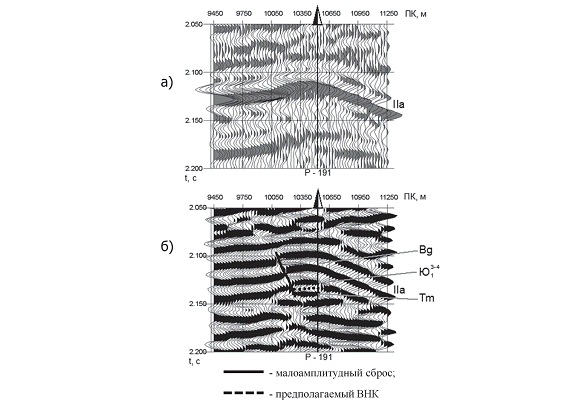
Рис. 9. Осложнение волновой картины, связанное с двухступенчатым тектоническим нарушением и ВНК (Крапивинское месторождение).

По результатам ГИС и исследования кернов, полученных на скважинах Крапивинского нефтяного месторождения Томской области, было выделено шесть типов геологического разреза, различающихся по пористости и проницаемости. Для сейсмотрасс, соответствующих положению скважин, был проведен ФАН-анализ и получены эталонные ФАН-образы для юрского продуктивного горизонта (рис. 10). Из рисунка видно, что ФАН-образы, принадлежащие различным типам геологического разреза, значимо различаются по своей структуре, что позволяет использовать их для классификации в межскважинном пространстве.

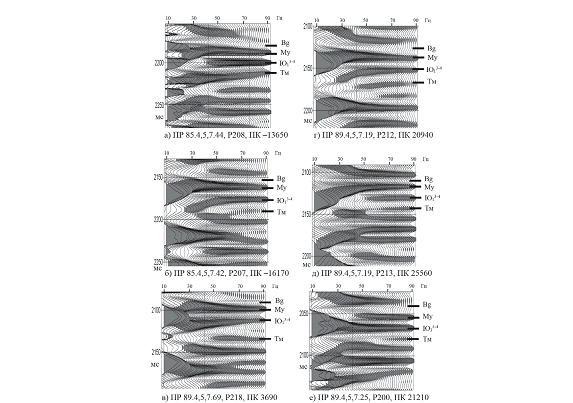
Рис. . Эталонные ФАН — образы для различных типов геологического разреза
а) I — тип; б) II — тип; в) III — тип; г) IV — тип; д) V — тип; е) VI — тип

Результаты проведенной обработки сейсмических материалов на ряде нефтяных месторождений Томского Приобъя подтверждают большую перспективность применения предложенных фазочастотных методов для решения структурных задач и задач прогноза геологического разреза.

Литература

1. Авербух А.Г. Изучение состава и свойств горных пород при сейсморазведке. М.: Недра, 1982.

2. Боганик Г.Н., Гурвич И.И. Сейсморазведка: Учебник для вузов. Тверь: Изд-во АИС, 2006.

3. Давыдова Е.А., Копилевич Е.А., Мушин И.А. Спектрально-временной метод картирования типов геологического разреза// Геофизика. 2002. № 5. С. 682–684.

4. Худзинский Л.Л. О частотно-фазовом анализе сейсмических волн// Динамика земной коры. М.: Наука, 1965. С. 65–70.

5. Иванченков В.П., Кочегуров А.И. Определение временного положения сейсмических сигналов по оценкам их фазочастотных характеристик // Геология и геофизика. 1988. № 9. С. 77–83.

6. Иванченков В.П., Шлотгауэр В.А. Применение спектральных характеристик для решения некоторых задач автоматической обработки сейсмограмм// Изв. вузов. Геология и разведка. 1977. № 3. С. 108–116.

7. Авербух А.Г., Трапезникова Н.А. Отражение и преломление плоских волн при нормальном падении на границу поглощающих сред // Изв. АН СССР. Физика Земли. 1972. № 9. С. 74–83.

8. Иванченков В.П., Кочегуров А.И., Орлов О.В. Фазочастотные характеристики сейсмических волн и основные предпосылки их применения для решения задач прогноза геологического разреза // Известия Томского политехнического университета. 2008. Т. 313. № 5. С. 132–137.

9. Иванченков В.П., Кочегуров А.И., Орлов О.В. Исследование разрешающей способности методов фазочастотного прослеживания сейсмических сигналов // Известия Томского политехнического университета. 2012. Т. 320. № 5. С. 80–84.

10. Иванченков В.П., Кочегуров А.И., Купина Н.А., Орлов О.В. Методы фазочастотного прослеживания отраженных волн и их применение в задачах обработки сейсмической информации // Технологии сейсморазведки. 2013. № 3. C. 5–10.

__________________________________________

ИВАНЧЕНКОВ Виктор Павлович

Кандидат технических наук, доцент кафедры прикладной математики Национального исследовательского Томского политехнического университета

КОЧЕГУРОВ Александр Иванович

Кандидат технических наук, и.о. заместителя директора института кибернетики по научной работе Национального исследовательского Томского политехнического университета

ОРЛОВ Олег Викторович

Кандидат технических наук, доцент кафедры прикладной математики Национального исследовательского Томского политехнического университета