К основам устойчивости и целенаправленности функционирования систем поддержки решений. Часть II. Целенаправленность
Райков А.Н.

---

При оценке влияния хаотичности и порядка на устойчивость функционирования информационных систем поддержки решений (СПР) в первой части статьи характеристика целенаправленности принятия решения во внимание почти не принималась – основной акцент делался на рассмотрение устойчивости состояния систем. Теперь сосредоточим внимание на необходимых условиях поддержки целенаправленности принятия решений. При этом будем считать понятия целенаправленности и целеустремленности функционирования систем [1] синонимичными.

Целенаправленность принятия решений больше ассоциируется с порядком, логикой, формализмами в поведении системы, со сходимостью процесса принятия решений к некоторому благоприятному результату. Под целью следует понимать предвосхищение в сознании лица, принимающего решение (ЛПР), некоего идеального образа, феномена или желаемого состояния исследуемой ситуации в будущем. Цель может быть и недостижимой в обозримое время – тогда важность представляет общая направленность движения, тенденция. Формирование (поиск) цели, как правило, происходит с учетом предыдущего опыта и истории, однако не всегда происходит «по аналогии» с имевшими место случаями, не обязательно носит экстраполяционный и, тем более, монотонный характер. Аналогичные ситуации в накопленном опыте могут быть и не найдены, однако опыт поиска цели и решения проблемы может пригодиться всегда.

При поиске цели важнейшей характеристикой считается оперативность ее выбора (принятия решения «Что делать?»). Например, в предпринимательской среде в критической ситуации скорее выиграет тот, кто быстрее примет решение – при метаниях в поисках цели обычно выигрывает конкурент.

Цель сама по себе обычно не поддается формализации. Она идеальна, латентна, и, скорее, является атрибутом мысли, рассудка ЛПР. Цель в сочетании с ее формализованным представлением (осуществлением, эксплицией) – это уже скорее идея¹. Функционирование СПР начинается с проявления идеи – осуществления цели. Об применении СПР вообще есть смысл говорить только при условии, что цель как-то эксплицируется, ищется ее осуществленное значение, определяется ее взаимосвязь с ситуацией, объектом и средством (инструментом) управления. Всегда нужен предмет исследования, а также возможность осуществления коммуникаций при групповом (кооперативном) принятии решений. В противном случае цель остается «вещью в себе», а СПР – вырожденной.

С учетом понятия цели СПР – это информационная система, которая на базе применения интеллектуальных информационных технологий обеспечивает ЛПР информацией и методологическими знаниями для эффективного принятия целенаправленных решений [4, 5, 6]. Для системного определения места СПР при принятии решений проведем декомпозицию процесса управления (рис. 1).

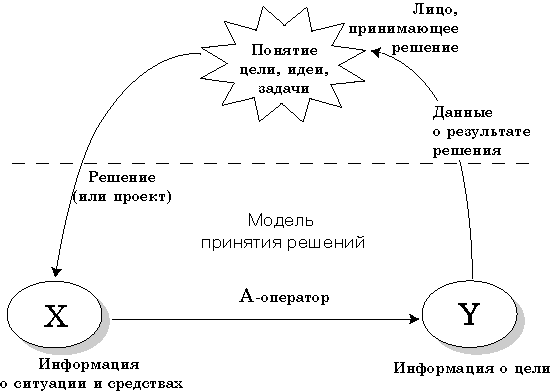
Рис. 1. СПР охватывает все компоненты процесса управления

В основе создания современных СПР лежат информационные технологии, реализующие интерактивное моделирование ситуаций и поддержку принятия решений на базе средств и методов искусственного интеллекта. При этом предполагается активное участие в процессе принятия решений ЛПР. В этом процессе помогают также методы и средства компьютерной поддержки режима «виртуальной реальности».

Если для разрешения рассматриваемой ситуации или решения конкретной задачи имеется относительно большой предшествующий опыт, то моделирование на базе интеллектуальных информационных технологий принципиального труда не составляет – компьютер можно обучить, построить базу данных и знаний. Но тогда моделирование уже трудно ассоциировать с понятием интеллектуальное – это для разработчика технологии. Для пользователя же замена живого специалиста-эксперта компьютером еще долго может ассоциироваться с чудом.

И все же область интеллектуальных информационных технологий – это, прежде всего, нетривиальные мыслительные процессы, носящие слабопредсказуемый творческий характер, подчиняющиеся невидимой логике, интуиции, здравому смыслу, а также операции целеполагания в нестандартных критичных природных и техногенных ситуациях. Средства и методы интеллектуальных информационных технологий сводятся к таким, ставшим уже широко известными, понятиям, как экспертные системы, когнитивные технологии, эволюционные системы, нейронные технологии, генетические алгоритмы, нечеткие системы. Иногда эти дисциплины в сочетании с вероятностными методами сводятся к единому понятию «мягкие вычисления» (Soft Сomputing) [7].

В том или ином виде функционирование интеллектуальных информационных технологий связано с достижением какой-либо не всегда очевидной цели, получением доступных благоприятных результатов. Как известно, в этой научно-практической области имеются весомые результаты, разработаны и пользуются большим коммерческим успехом соответствующие интеллектуально-информационные продукты (технологии).

Вместе с тем, для информационно-открытых проблемных областей, предметом которых являются хаотичные и неустойчивые ситуации, достигаемая цель неопределенна и зависит от времени, промежуточных результатов, характеризуется огромным числом признаков и пр. – традиционные интеллектуально-информационные подходы не пользуются особым доверием. Тогда пользователю остается больше полагаться на свою исключительную интуицию, «провидение», «здравый смысл» и пр. Значение этих «методов» мы не умаляем, однако наша задача – способствовать, чтобы «здравый смысл» в социально-ответственных проблемных ситуациях чаще «попадал в цель».

Итак, у ЛПР отсутствует уверенность в том, что в достаточно сложных ситуациях подход с использованием СПР содействует как поиску, так и достижению благоприятных целей, получению достаточно хороших (не обязательно оптимальных) решений за заданное время. Причем, как показывает практика, эта уверенность совсем пропадает при наличии латентных (скрытых, закрытых, непонятных) факторов, характеризующих исследуемую ситуацию. Особенно этим отличаются политические ситуации, ситуации, отражающие корпоративные интересы.

По нашему мнению, чтобы убедить лица, принимающие решения, в пользе СПР, необходимо снабдить их рядом достаточно общих рекомендаций (принципов, критериев), с помощью которых можно оперативно оценивать успешность своих действий на промежуточных этапах принятия решений и обеспечивать тем самым устойчивость и целенаправленность управления ситуацией. Скорее всего, это больше касается таких аспектов процесса, которые ЛПР понятны, доступны и на которые он может воздействовать. К таким аспектам относятся: структуризация имеющихся информации и данных, последовательность отдельных действий (операций), контроль соответствия имеющихся возможностей (полномочий, времени и денег, доступа к информации и пр.) предвосхищаемым целям.

Неуверенность ЛПР порождается наличием трудностей понимания возможности получения благоприятных результатов в тех или иных непростых ситуациях за счет использования накопленного методологического опыта принятия решений. Особую трудность вызывают ситуации, характеризующиеся неустойчивыми скачкообразными изменениями их характеристик (резкими переходами значений параметров), происходящими в процессе непрерывного развития (эволюции) этих ситуаций. К таким случаям следует отнести возможные плохо предсказуемые скачкообразные особенности формирования социумов, фондовых рынков, резкие переходы в создании социально-экономических формаций и др.

Для анализа и предсказания возможных тенденций развития процессов в скачкообразных ситуациях помогает методология теории катастроф [8, 9]. Она помогла классифицировать и типизировать возможные скачки и тем самым снизить неопределенность предсказания возможных последствий принятия решений и направлений развития ситуаций даже в условиях, когда не известны закономерности развития исследуемых процессов. Однако при этом вопрос с оценкой целенаправленности (включая сам поиск цели) развития событий на базе применения СПР остается, в целом, открытым.

Так, в информационно-открытой проблемной области на процесс решения задач существенное влияние оказывают внутренние и внешние хаотические тенденции, непредсказуемая интуиция человека – их как-то надо учитывать в работе СПР. Хаотические тенденции мы попытались в первой части статьи локализовать до оценки их влияния на устойчивость состояния СПР без учета влияния на целенаправленность принятия решений. Формализованный же учет человеческого фактора требует отдельного рассмотрения – ведь именно человек в конечном итоге определяет целенаправленность функционирования СПР – даже если различные методологические приемы поисковой оптимизации (термодинамические [10], диффузионные [11], случайные [12] и подсказывают наилучшие направления развития хаотической ситуации.

Если на процесс решения задач непосредственное влияние оказывает человек, то он (имея цель) привносит в процесс направляющее воздействие, рассуждая больше качественно, чем формально. Здесь важнейшая функция человека – уйти от бессмысленных метаний в поиске ответа, «удержать» процесс решения от неконтролируемых скачков при неожиданных изменениях исходных данных и «дрейфе» цели – сделать процесс решения более целенаправленно устойчивым, т. е. обеспечить поиск и достижение цели в заданное время, меньшей ценой и без скачков. Этому и предназначены служить СПР, обеспечивающие сходимость ситуации к желаемой цели за счет принятия корректной серии достаточно хороших решений [13].

Фундаментальное значение при построении СПР для информационно-открытых проблемных областей, по нашему мнению, приобретают методы решения задач, позволяющие использовать качественные знания ЛПР. Для формализованной интерпретации целенаправленного процесса принятия решений в неустойчивых ситуациях воспользуемся результатами известных работ по методам решения некорректных задач [14, 15, 16]. Это круг задач, где при незначительном изменении исходных данных результат решения может меняется относительно сильно, а исходные данные (включая целевые) известны не точно. Желаемый эффект здесь достигается за счет соответствующей структуризации исходных данных и предоставления возможности исследователю определенным образом интерактивно влиять на процесс принятия решения, используя при этом как качественную, так и количественную информацию. К формированию методов решения некорректных задач подошли сравнительно давно [17, 18, 19], однако, как показывает реальная практика, возможности этого подхода далеко не исчерпаны.

Будем исходить из того, что информацию о любой ситуации или управляемом объекте можно представить (эксплицировать, формализовать) через множества известных сведений о них (неопозитивистский взгляд на представление смысла высказываний [20, 21]). Любая ситуация характеризуется признаками (свойствами), проявляющимися при взаимодействии с ее внешним окружением (другими объектами) и доступными для восприятия СПР. Смысловое наполнение признака представим экстенсионально через сведение – некоторое множество других ситуаций (объектов), обладающих одинаковым свойством. Например, сведениями о некотором человеке могут быть выражения «Ему сорок лет», «Он научный работник» или «Он государственный служащий» – эти сведения представляются множествами соответствующих людей. Причем, говоря о признаках, сведениях и свойствах, мы не акцентируем внимание на их ранжировании, оценке и выделении наиболее важных. Такая оценка может быть проведена только при наличии каких-то критериев, цели исследования. А это уже уровень понятия информации – более комплексного понятия.

Для представления некоторой информации о ситуации (объекте) одного сведения уже мало – желательно, чтобы сведений было несколько, они как-то «пересекались», и, переходя через меру сведений и свойств, давали бы новое качество. Когда говорят об информации, больше думают об устранении дефицита сведений об объекте для достижения какой-то цели, принятия некоторого решения. Информация больше ассоциируется с целенаправленными процессами принятия решений. Например, множество людей определенного возраста, социального положения и образовательного уровня могут рассматриваться в качестве кандидатов на вакантную должность в министерстве.

Всякое сведение должно иметь имя, которое идентифицирует ситуацию (объект). Имя – это параметр модели. На рис. 1 представления имен объектов находятся под пунктирной линией (сущностная декомпозиционная область). Сведение об объекте предполагает некую прагматику, то есть сведению должно соответствовать некоторое понятие в сознании ЛПР (это еще не цель) – на рис. 1 оно представлено над пунктирной линией (понятийная область).

Формально выделяется три основных структуры: сведение, данные и информация². Сведение об объекте с именем x₀НX представляется множеством – обозначим его x(x₀). Данные об объекте – более сложное понятие – это семейство сведений {x_i(x₀)}, где i=1,...,Ґ. Информация об объекте – это то общее, что несут в себе различные данные об одном и том же объекте, но уже относительно некоторой цели. Информация формально представляется совокупностью всех признаков и свойств ситуации, сформированных в целенаправленном процессе взаимодействия структур данных о ней с внешним окружением. Проблемной ситуации имманентно присуща целенаправленность – в противном случае не было бы такой ситуации.

Различные данные могут нести для ЛПР одну и ту же информацию. Например, информация о благополучии одной и той же социально-экономической ситуации может быть задана различными наборами данных: значением статистических показателей, фотографиями, сравнительным текстовым описанием и др. Целевая установка для проведения оценки ситуации и принятия решения в этом примере кроется за понятием «благополучие». Информацию в массе имеющихся потоков сведений вообще можно «различить» только при наличии определенной цели.

Для демонстрации оттенков различия между данными и информацией удобно применять различные аналогии. Например, при обращении к биологии понятию информации больше соответствует уровень представления фенотипов³, а свойствам, сведениям и данным – генотипов⁴. Однако переход между уровнями фенотипов и генотипов достаточно «размыт». В природе однозначного соответствия между генотипом и фенотипом некоторой особи (организма) нет. Естественный отбор особей идет по фенотипу (где несомненную роль играют цели и решения) при наличии разнообразия генотипов. Закономерности эволюционного развития организмов успешно используются для разработки достаточно прогрессивных информационно-интеллектуальных методов эволюционного моделирования сложных ситуаций. При этом представления фенотипов строят над пространством генотипов [22].

Возможность представления информации и ее обработки (включая логическую или стохастическую) на базе семейств множеств позволяет использовать имеющиеся математические инструменты для повышения эффективности принятия решений в информационно-открытых проблемных областях. Очевидно, учитывая специфику таких проблемных областей, изложенные ниже конструктивизмы носят больше интуиционистский характер [23], претендуют только на прояснение целенаправленных действий ЛПР, и, в то же время, позволяют сформировать искомые рекомендации ЛПР для повышения доверия к системам поддержки решений.

Обозначим данные (а затем и информацию) о ситуации или объекте x₀ через Б(x₀) – они выражаются через семейство сведений {x_i(x₀)}. При этом данные «несут» некоторую информацию, если их можно как-то оценить или упорядочить с учетом сопоставления с другими данными, характеризующими какую-либо цель. Вместе с тем любое упорядочение данных, отражающее некоторую закономерность (например, даже парадигму или синтагму), уже несет в себе определенную информацию. Чтобы можно было говорить о самой элементарной информации, используем следующее минимальное упорядочение сведений и данных. Пусть для сведений {x_i(x₀)} об информации Б(x₀) выполняются следующие условия:

из x(x₀)МБ(x₀) следует x(x₀)№Ж (осуществленность – представимость сведений в сущностной декомпозиционной области, см. рис. 1),

из x(x₀)МБ(x₀) следует x‘(x₀)МБ(x₀) для любого x‘(x₀)Йx(x₀), x‘(x₀)МX (вложенность – наличие осуществленной связи сведений и информации),

из x₁(x₀)МБ(x₀) и x₂(x₀)МБ(x₀) следует x₁(x₀)&x₂(x₀)Мc(x₀) (накапливаемость – из различных сведений складывается информация).

Заметим, что мы не требуем, чтобы на этих множествах была бы обязательно задана какая-нибудь метрика – для оценки, например, «близости» точек. Ведь близость точек может быть задана и с помощью понятия их окрестностей, принадлежности точек одному множеству, транзитивной или толерантной близости и пр. В этих случаях удобно использовать возможности общей топологии [24, 25].

Если для семейства множеств {x_i(x₀)}НБ(x₀) выполняются перечисленные условия, то такой ситуации в общей топологии соответствует определение фильтра, сходящегося к точке – это представление элементарной информации. В дальнейшем изложении, говоря о точке x, мы всегда будем иметь в виду элементарную информацию о ней – поэтому символ Б при обозначении информации о точке, как правило, будем опускать.

Пусть xНX – информация о конкретной ситуации (внутренней и внешней) и имеющихся средствах достижения различных целей (возможностях воздействия на ситуацию), yНY – имеющаяся информация о цели ЛПР. Оператор А осуществляет связь Аx=y, где информация y есть следствие, причинно обусловленное заданием оператора А и информации x.

В реальной практической ситуации все параметры уравнения Аx=y имеют приближенное значение, а иногда и попросту не определены и подлежат поиску. При этом наиболее рискованными считаются начальные этапы решения задач. Для большинства задач естествознания прямое измерение x вообще невозможно, а для информационно-открытых проблемных областей с преимущественно качественным характером сведений, данных и информации об измерении параметров говорить вообще не приходится. И, несмотря на большой риск начальных этапов, ограниченность исходных данных и времени, большую неопределенность целей – в любом случае необходимо введение искусственных приемов и ограничений.

Поясним понятие неопределенности, приближенности значений исходных данных для известного случая метризуемых пространств X и Y. Предположим, что некоторой конкретной информации о состоянии ситуации и имеющихся средствах x₁НX соответствует некоторая информация о цели – элемент y₁=Аx₁НY. Допустим, что нам стали доступны только приближенное значение элемента y₁:y_dНY и оценка его точности d – расстояние в заданной метрике r_y(y₁,y_d)Јd. Причем, неточных значений y_d может быть получено несколько. Возникает необходимость решения обратной задачи: по совокупности известных {y_d} найти x_1. Тогда основные возникающие проблемы можно охарактеризовать следующим образом:

исследовать вопрос о сопоставимости А информации {x_d}НX приближенным значениям {y_d}, т. е. найти модель {x_d}НX такую, что r_y(Аx_d,y_d)Јd, когда x_d®x_d при d®0;

определить погрешность приближенного решения в рамках принятой модели, т. е. оценить в заданной метрике расстояние от x_d до элемента x₁..

Методические сложности при решении любых обратных задач возникают в связи с тем, что обратный оператор А^-1, заданный на всей своей области определения АX=Y, не является непрерывным (малые возмущения y могут сопровождаться большими отклонениями решений x). В связи с этим задачи делятся на корректные и некорректные. Характерным для корректных задач (Ж. Адамар, 1902) является наличие следующих признаков решения: существования (для всякого элемента y₁ существует решение x₁), единственности (решение определяется однозначно), непрерывности (решение задачи устойчиво на пространствах X и Y, т. е. малым возмущениям y соответствуют малые отклонения решений x).

В корректных задачах за приближенное решение можно принять элемент x_d=А^-1y_d так как x_d®x₁ при d®0. Долго существовала точка зрения, согласно которой только корректные задачи адекватны реальной действительности. Однако жизнь «подбрасывала» проблемы, не удовлетворяющие условиям корректности. Например, поиск полезных ископаемых, социальные кризисы, экологические катастрофы. Поэтому к некорректному классу задач относятся и задачи, возникающие в информационно-открытых проблемных областях.

При поддержке принятия решений с помощью СПР, построенных на базе интеллектуальных информационных технологий, очевидно, некоторые (не обязательно все) из перечисленных условий корректности могут быть не выполнены. Тогда, например, если первое и третье условие не выполняются, то элемент x_d=А^-1y_d даже если он и существует, не является приближенным решением, так как x_dпри малых d может сколь угодно сильно уклоняться от точного решения.

Для решения некорректных задач на метризуемых пространствах разработаны различные подходы, например, метод регуляризации, который позволяет строить эффективные численные алгоритмы решения. Так, введено понятие регуляризующего оператора R, который, действуя при определенных условиях из пространства Y в пространство X, каждой паре (y_d,d) ставит в соответствие элемент x_dНX такой, что x_d®x₁ при d®0 (⁵). Метод регуляризации успешно работает в таких проблемных областях, как физика плазмы, обработка изображений и др., т. е. там, где можно ввести метрику или стоит задача численной параметрической оптимизации. В таких задачах параметры, как правило, явно характеризуют схему управляемого объекта или суть проблемной ситуации, а признаковые пространства сравнительно небольшие.

В общем же случае, включая случай с информационно-открытыми проблемными областями, когда информация об объектах представляется семействами множеств, а метрику, адекватную реальной ситуации, ввести не всегда представляется возможным, традиционный, например, регуляризующий метод впрямую не помогает.

Пусть информация, данные и сведения о y₁ представляются через семейства множеств типа {b_n(y₁)}НБ(y₁), где n – индекс из частично упорядоченного множества. Аналогичное представление допустим и для x_1. Пусть также цели являются физически достижимыми при заданных ресурсах, хотя точно и не известными. Формально эта достижимость представляется в виде «покрытия» множеством AX всего множества целей Y, что требует соответствующих представлений и интерпретации оператора отображения информации А, информации о ситуации и имеющихся средствах (множество X), а также информации о цели (множество Y). Поскольку область значений AX – суть точки, сведения о которых несут непустые подмножества множества Y (окрестности этих точек), то такой ситуации в общей топологии соответствует понятие плотности отображения: AX всюду плотно в Y, если его замыкание совпадает с Y при AXЙY. Доказано, что множество AX всюду плотно в Y тогда и только тогда, когда любое непустое открытое подмножество Y содержит точки множества AX [22].

Из плотности множества AX в пространстве Y следует, что каждая окрестность b_d(y₁)Нb_n(y₁) имеет непустой полный прообраз А^-1b_d в X. В нашем случае представления информации на базе семейств множеств (непустых окрестностей точек) понятие корректности задач можно определить следующим образом [26].

Пусть {b_d} – фильтр окрестностей точки y₁. Будем говорить, что задача решения уравнения AX=Y при y=y₁ поставлена корректно в некоторой топологии, если:

1) пересечение прообразов ф_dA^-1b_d содержит лишь одну точку x₁ (существование и единственность решения);
2) фильтр полных прообразов А^-1b_d в X сходится к x₁ (непрерывность).

В приведенном определении не требуется, чтобы сколь угодно близко от точки y₁ находились точки, не имеющие прообразов в X. Поэтому «близкие» к y₁ точки могут являться «возмутителями» корректности: точками скачков, источниками неустойчивости решения, точками повышенной чувствительности к изменениям исходных данных.

Пусть y₁НY при отображении AX®Y имеет в X единственный прообраз x₁ (выполнено первое условие). Тогда, задача может состоять в следующем: требуется сопоставить каждому элементу окрестностей точки y₁ такую точку x_dНX, что x_d®x_1. Если же для этой задачи не выполнено второе условие, то для нее методы решения некорректных задач на метризуемых пространствах неприменимы. Однако такие задачи могут быть решены при определенных достаточно общих предположениях и требованиях к структуре отображаемых пространств. Как известно [23], одним из путей решения таких задач является сужение области определения оператора А на бикомпактное множество MМX (⁶), что в предположении замкнутости графика отображения А (⁷), хаусдорфовости пространств X и Y (⁸) и плотности [22] множества значений оператора A позволяет применять методы решения некорректных задач, используемые для метризуемых пространств. Перечисленные требования к отображению А, структуре и форме представления пространств X и Y являются необходимыми условиями обеспечения устойчивой сходимости процесса решения задачи к некоторой плохо определенной цели. Их информационная интерпретация собственно и должна лежать в основе формирования искомых для обеспечения устойчивости и целенаправленности управления на базе СПР.

Показано, что график непрерывного отображения замкнут [28], а отсюда следует, что замкнутые отображения являются обобщением непрерывных. Интуитивная интерпретация операции замыкания множества элементов отражает установление неявных (например, транзитивных, толерантных, логических и др.) взаимосвязей элементов. Через замыкание некоторого множества элементов, являющегося сведением об этих элементах, можно определить информацию об этих элементах. При этом заметим, что операция замыкания для множеств-сведений хорошо ассоциируется с определенным выше условием вложенности сведений.

Остановимся, в качестве примера, более подробно на интерпретации понятия бикомпактности. Как отмечено выше (см. ⁵), топологическое пространство называется бикомпактным тогда, когда из каждого его открытого покрытия можно выбрать конечное подпокрытие. Для интерпретации понятие бикомпактности удобно ввести через понятие центрированного семейства множеств [22]. Семейство множеств называется центрированным тогда и только тогда, когда пересечение любого конечного множества элементов этого семейства не пусто. Используя понятие центрированного семейства множеств, необходимые и достаточные условия бикомпактности семейства множеств сводятся к условию: топологическое пространство бикомпактно тогда и только тогда, когда каждая центрированная система замкнутых в нем множеств имеет непустое пересечение. Или – топологическое пространство бикомпактно тогда и только тогда, когда каждая направленность в нем имеет предельную точку.

Эти условия можно интерпретировать в терминах конкретных прикладных ситуаций, возникающих при принятии решений. Рассмотрим простой пример: стоит задача поиска информации в «необъятном» массиве книг, журнальных статейи их фрагментов (документов) большой библиотеки (множество X), причем исследователь не очень точно представляет, какой текст ему нужен (обычная неясность цели – на множестве Y). Тогда модель пространств (X, Y) для решения задачи изначально представляет собой условно-бесконечную (необозримую в заданное время) совокупность элементов – документов и потребностей. Пусть для нахождения решения задачи возможно проведение итерационной выборки некоторых подмножеств релевантных документов. Очевидно, что задача будет иметь только тогда корректное решение, когда все альтернативные варианты можно либо упорядочить и эту упорядоченность направить к некоторому конечному результату (пределу), либо выбрать некоторое обозримо-конечное число вариантов решения (релевантных подмножеств), которые можно оценить по какому-нибудь (например, интуитивно) критерию. И тот и другой случай отвечают условиям бикомпактности пространства документов X.

Эти рассуждения могут носить также следующий характер. Поскольку множество возможных вариантов решения задачи строится на основе выбора обозримо-конечного набора документов, то выбираемое подмножество наиболее релевантных документов VМX, на котором строятся ответы, должно отвечать требованию бикомпактности. Тогда все документы, не входящие в множество V, будут являться дополнением к нему и состоять преимущественно из нерелевантных документов. В противном случае будет иметься комбинация документов, состоящая из релевантных документов, не входящих в подмножество V, – что не удовлетворяет условию бикомпактности. Таким образом, содержательно бикомпактность характеризует полноту (представительность) множества найденных документов и определяет оперативность поиска (за счет упорядочения поиска) [29]. Совсем простой способ интерпретации понятия бикомпактности на этом примере – это систематизировать имеющийся массив документов по тематическому классификатору, имеющему упорядоченный набор рубрик. Заметим, что для представлений поисковых предписаний такое ограничение не обязательно.

С учетом изложенного предложим следующий набор принципов-критериев по организации процессов обработки информации при принятии решений на базе СПР (далее – процессов), существенным образом определяющих устойчивость и целенаправленность процессов в информационно-открытых проблемных областях [30].

1. Информационная открытость проблемных процессов по отношению к внешнему окружению способствует повышению устойчивости функционирования СПР. При этом систематизация информации, интенсивность ее поступления и обработки на всех уровнях должны контролироваться ЛПР. Вместе с тем излишняя открытость может привести к снижению целенаправленности, и даже – хаотической деградации процессов.

2. В СПР должны быть заложены формализованно-структурные механизмы анализа и прогноза внутренней и внешней ситуации. При явной недостаточности информации для принятия решений эти механизмы должны опираться на кооперативные интеллектуально-экспертные процедуры.

3. В СПР должны быть предусмотрены иерархические информационно-управляющие структуры. Они строятся по правилу: снижение требований к точности обработки информации и повышение возможности доступа к исходной информации с ростом уровня принятия решений. На каждом уровне необходимо учесть возможность спонтанных отклоняющих процессов.

4. При разрыве, ослаблении или изменении связей между уровнями управляющей структуры СПР должна сохранять «живучесть» – продолжать функционировать, хотя, возможно, с некоторой потерей эффективности. Однако введение для этого дублирующих связей не должно приводить к чрезмерным структурной жесткости и повышению хаотичности управления.

5. Функции СПР должны быть расклассифицированы по блокам (модулям). Причем модули эти должны обозримо-конечным образом «покрывать» всю проблемную область принятия решений. Модули информационно взаимодействуют между.

6. Желательно, чтобы число функций (элементов), из которых строятся модули, было условно-бесконечным: например, необозримым за время рассмотрения контролируемой ситуации. Функциональные возможности СПР должны быть достаточно разнообразны.

7. Определяются направления развития СПР, т. е. планируется разработка гипотетических (дополнительных) функций на отдаленную перспективу.

Очевидно, реальная практика много богаче рассмотренной нами попытки топологического представления ситуаций, задач, информации и данных. Например, исследования показывают, что в развитие вышесказанного заслуживают внимания прикладные исследования способов обеспечения сходимости решений некорректных задач на нечетких топологических пространствах [31, 32], дискретных пространствах [33] и др.

Таким образом, «метод здравого смысла», который зачастую кладется в основу принятия решений в той или иной сложной обстановке, с большим успехом приведет к благоприятному результату, если его применять с учетом фундаментальных закономерностей информационных преобразований, способствующих повышению устойчивости, целенаправленности и оперативности принятия решений.

---

^* Часть I. «Устойчивость» данной статьи опубликована в журнале «Информационное общество», 1997, № 4–6, с. 56–60.

¹ Идея связывается с «сознанием цели» и проекцией по преобразованию мира [2], тождеством «созерцания и понятия», «сущности и цели», образующих «целостность органического» [3].

² Используемые далее обозначения X, Y и A соответствуют рис. 1. Идея различения сведений, данных и информации подсказана автору А. В. Чечкиным [14] (прим. автора).

³ Фенотип - совокупность всех признаков и свойств организма, формирующихся в процессе взаимодействия его генотипа и внешней, по отношению к нему, среды (прим. автора).

⁴ Генотип - в узком смысле, это совокупности компонентов (аллей) генов, контролирующих некоторый признак организма (прим. автора).

⁵ За точное определение регуляризующего оператора можно взять: оператор R(y,d), действующий из пространства Y в пространство ММX называется регуляризующим для уравнения Аx=y (относительно значения y₁), если он обладает свойствами: 1) существует такое число d₁>0, что оператор R(y,d) определен для всякого d, 0ЈdЈd₁, и любого y_d такого, что r_Y(y_d,y₁)Јd; 2) для всякого e>0 существует d₀=d₀(e,y_d)Јd₁, такое, что из неравенства r_Y(y_d,y₁)ЈdЈd₀ следует неравенство r_M(x_d,x₁)Јe, где x_d=R(y_d,d) [12].

⁶ Топологическое пространство бикомпактно, если из каждого его открытого покрытия можно выделить конечное подпокрытие.

⁷ Множество G={x,Ax: xОX} в произведении XґY топологических пространств называется графиком отображения A. Отображение же A:X®Y называется отображением с замкнутым графиком, если: 1) график G отображения A есть замкнутое множество в XґY; 2) из того, что фильтр {x_d} на области определения O(A) оператора A сходится в X к x₁ОX и фильтр, порождаемый множествами Ax_dМY, сходится к y₁, следует x₁ОO(A), y₁=Ax₁ [23].

⁸ В хаусдорфовом топологическом пространстве любые две различные точки x и y имеют непересекающиеся окрестности [27].

---

Литература:

1. Акофф Р., Эмери Ф. О целеустремленных системах / Пер. с англ. под ред. И. А. Ушакова. // М.: «Советское радио, 1974. 272 с.
2. Философский энциклопедический словарь // М.: Советская энциклопедия, 1989. С. 207.
3. Гегель Г. Политические произведения. // М.: Наука, 1978. 437 с.
4. Klein M., Methlie L.B. Knolege-Based Desision Support Systems with Application in Business, 2nd edn (Wiley, 1995).
5. Zopounidis C., Doumpos., Matsansinis N.F. On the use of knowledge-based decision support systems in financial management: A survey. Desision Support Systems 20 (1997) 259–277.
6. Райков А. Н. Информационные системы поддержки государственных решений // Вестник РОИВТ –М: ВИМИ, 1995. № 5. С. 18–29.
7. Zadeh L.A. What is Soft computing?// Soft Computing. A Fusion of Foundations, Methodologies and Applications. –1997. –V. 1. –№ 1. –P 1.
8. Арнольд В. И. Теория катастроф // М.: Наука, 1990. 128 с.
9. Малинецкий Г. Г. Хаос. Структуры. Вычислительный эксперимент: Введение в нелинейную динамику. // М.: Наука, 1997. 225 с.
10. Raikov A. N, Ulyanov S.V. Fuzzy modelling of support decision as intelligent tech-nology in control of complicated social-political object// «Proceedings of the Int.Conf. on Applicatin of Fuzzy Systems» (ICAFS-94), University оf Tabriz, Iran, 17-19 October, 1994.- P. 281–283
11. Юдин Д. Методы количественного анализа сложных систем. // Изв. АН СССР. Сер. техн. киберн., 1966, № 1. С. 3–16.
12. Rasrigin L. A. Random Search in Evolutionari Computatio. –First International Conference on Evolutioary Computation and Its Application, 1996, p. 135–142. Publisher: EvCA’96.
13. Райков А. Н. Сходящиеся информационные технологии проектирования функциональных задач // Информатика. Сер. Информационные технологии, средства и системы, 1990. № 1. С. 43–49.
14. Некорректные задачи естествознания /под ред. А. Н. Тихонова, А. В. Гончарского. // М.: Изд-во Моск. ун-та, 1987. С. 299
15. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. // М.: Наука. Гл. ред. физ.-мат. лит, 1986. 288 с.
16. Чечкин А. В. Математическая информатика // М.: Наука. Гл. ред. физ.-мат. лит, 1991. 416 с.
17. Новиков П. С. О единственности обратной задачи теории потенциала // Доклады Академии наук СССР, 18, 1938. № 3. С. 195–198.
18. Тихонов А. Н. Об устойчивости обратных задач // Доклады Академии наук СССР, 39, 1944. № 5. С. 195–198.
19. Иванов В. К. О линейных некорректных задачах // Доклады Академии наук СССР, 145, 1962. № 2. С. 270–272.
20. Панова Н. С., Шрейдер Ю. А. Принцип двойственности в теории классификации // НТИ. Сер. 2, 1975. С. 3–10.
21. Райков А. Н. Алгебраическая симантика булевого поиска документов // НТИ. Сер. 2, 1990. № 5. С. 27–30.
22. Shaffer J. D., Eshelman L. J. Combinatorial Optimization by Genetic Algoritms^ The Value of the Genotype/Phenotype Distinction. –First International Conference on Evolutioary Computation and Its Application, –1996, –p. 110–120. Publisher: EvCA’96.
23. Голдблат Р. Топосы. Категорный анализ логики: Пер. с англ. // М.: Мир, 1983. 488 с.
24. Келли Дж. Общая топология. / Пер. с англ. А. В. Архангельского. 2-е издание // М.: Наука. Гл. ред. физ.-мат. лит, 1981. 432 с.;
25. Энгелькинг Р. Общая топология / Пер. с англ. М. Я. Антоновского и А. В. Архангельского // М.: Мир. 1986. 752 с.
26. Иванов В. К. Некорректные задачи в топологических пространствах // Сибирский математический журнал, 1969. т. Х. С. 1065–1074.
27. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. 6-е издание. // М.: Наука. Гл. ред. физ.-мат. лит, 1989. 624 с.
28. Бурбаки Н. Основные структуры анализа. Теория множеств. Пер. с франц. / Под ред. В. А. Успенского. // М.: Мир, 1965. 455 с.
29. Райков А. Н. Условия предельной сходимости диалогового поиска документов // НТИ. Сер. 2, 1990. № 3. С. 15–17.
30. Райков А. Н. Информационные факторы устойчивого управления социально-политическими ситуациями // Проблемы информатизации. 1995, вып. 2–3. С. 19–23.
31. Goguen J. A. The Fuzzy Tyhonoff Theorem // J. Math. Anal. Appl. –1973. –V. 43. –P. 734–642.
32. Pao-Ming P., Ying-Ming L. Fuzzy Topology I. Neighborhood Structure of Furry Point and Moor-Smith Convergence //J.Math. Anal.Appl. –1980. –V. 76. –P. 571–599.
33. Gahler S. Discrete convergence. Convergence Structures//Mathematic Research. –1985. –V.24. –p. 127–136.

---

Об авторе:

Райков Александр Николаевич - профессор, доктор технических наук

---

&copy Информационное общество, 1999, вып. 3, с. 27 - 34.