Методы оценки характеристик Российской автоматизированной системы информационно-правового обеспечения
Саксонов Е.А., Хургин В.М.

Рассказывается об использовании методов математического моделирования для оценки характеристик и обоснованного выбора структуры Российской автоматизированной системы информационно-правового обеспечения.

Российская автоматизированная система информационно-правового обеспечения правотворческой и правореализационной деятельности, правового образования и воспитания (РАСИПО) характеризуется исключительной сложностью, определяемой большим числом и высокой степенью взаимосвязи элементов и выполняемых ими операций, сложностью алгоритмов выбора тех или иных управляющих воздействий и большими объемами перерабатываемой информации [1].

Важнейшим элементом РАСИПО является интегрированная сеть связи, обеспечивающая функционирование территориально распределенного банка правовой информации. При этом с целью выполнения требований по пропускной способности и надежности функционирования системы высшие органы государственной власти и узлы правовой информации необходимо объединить в полносвязную глобальную вычислительную сеть по принципу "каждый с каждым". На втором уровне РАСИПО, т. е. внутри регионов, целесообразно использовать в основном радиальный (сеть типа "звезда") принцип связи абонентов с региональным узлом [2].

Способы гибкого объединения разнотипного вычислительного оборудования в единую коммуникационную среду реализуются в рамках неоднородных сетевых архитектур, наибольшее признание среди которых получила сетевая архитектура взаимосвязи открытых систем (ВОС) или открытых вычислительных сетей (ОВС). В такой архитектуре используется понятие системы - логического объекта, представляющего собой автономную совокупность технических и программных средств. Реальным представлением системы могут быть ЭВМ, многомашинный комплекс, абонентский пункт, концентратор и т. п., при этом основной особенностью последних является передача информации на большие расстояния независимым устройствам, что позволяет распределить вычислительные мощности, а не концентрировать их в одном месте. При этом каждая из взаимодействующих платформ рассматривается как открытая система, удовлетворяющая некоторому набору стандартных соглашений (протоколов).

Сеть РАСИПО охватывает всю территорию России и состоит из локальных сетей регионального и ведомственного уровней, связанных в единую глобальную сеть с использованием высокоскоростных широкополосных каналов связи.

Для оценки характеристик РАСИПО и обоснованного выбора структуры системы предлагается использовать математическое моделирование. В настоящее время известно достаточно большое количество публикаций, в которых рассмотрены математические модели распределенных вычислительных систем (сетей) различного назначения, позволяющие проводить расчет и оценку их эксплуатационных характеристик [3, 4, 5]. Как правило, эти модели позволяют либо достаточно точно исследовать относительно простую (и небольшую по размерности) реальную вычислительную систему, либо исследовать сложные системы, но с большой погрешностью (на качественном уровне). В нашем случае в качестве объекта исследования выступает крайне сложная система большой размерности, включающая в себя разнотипные сети, каналы связи, средства защиты информации и прочие факторы, учесть совокупное влияние которых на характеристики системы при аналитическом моделировании не представляется возможным. Целесообразно применить математическое моделирование для качественного анализа системы, выявления ее фундаментальных особенностей (например, направления изменений характеристик в зависимости от различных параметров). В сочетании с данными, полученными в ходе опытной эксплуатации отдельных элементов системы, результаты моделирования могут оказаться полезными при выборе направлений совершенствования системы.

Таким образом, целью математического моделирования является проведение качественного анализа сложной распределенной вычислительной системы (РАСИПО) с определением степени влияния параметров системы на ее характеристики.

В качестве математической модели системы используется замкнутая сеть массового обслуживания (ЗСеМО), что соответствует известным подходам и результатам анализа подобных систем [6, 7, 8].

В общем случае всю систему можно представить в виде набора источников различных типов (центральный и региональные узлы правовой информации, абонентские пункты, другие пользователи), сети передачи данных (с возможным включением различных по характеристикам подсетей) и набора серверов (обслуживающих запросы устройств), обрабатывающих разнотипные запросы. Обобщенная структура системы приведена на рис. 1.

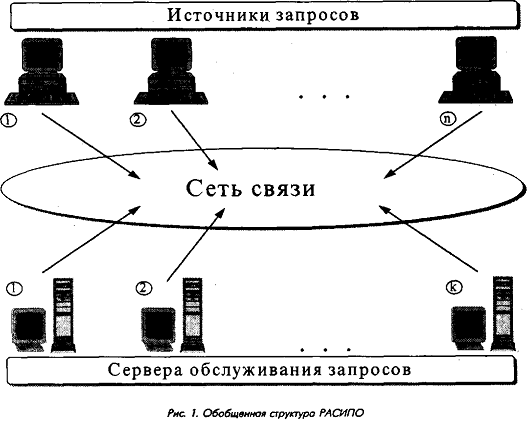
Поскольку в реальной системе источники запросов как правило не генерируют нового запроса до завершения обработки ранее введенного, общее количество запросов в системе ограничено и, следовательно, с большой достоверностью система может рассматриваться как замкнутая. Структура ЗСеМО, построенная на основе показанной на рис. 1 обобщенной структуры, представлена на рис. 2.

При построении аналитической модели сети массового обслуживания будем полагать, что времена передачи сообщений по каналам связи являются слабокоррелированными величинами. Это вполне соответствует действительности (применительно к исследуемой системе) в силу того, что на практике используются скоростные каналы связи, сеть связи имеет достаточно большое количество возможных маршрутов доставки сообщений и, наконец, запросы представляют собой относительно короткие наборы данных, умещающиеся в один передаваемый пакет, и не требуют использования процедур сборки-разборки. В пользу допущения о независимости говорят и результаты исследований, приведенные в работе [6].

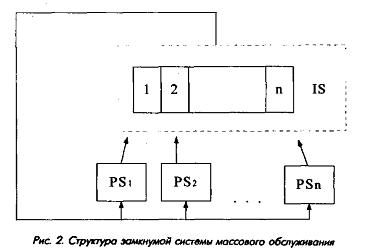
В обобщенной модели сеть передачи данных (включая телефонные, компьютерные и коммерческие сети) может быть представлена центром обслуживания типа IS (обслуживание без очередей) [6], который представляет собой многолинейный центр с числом обслуживающих приборов, соответствующим (равным и большим) числу сообщений в системе (это обусловлено развитой структурой сети передачи данных, как отмечалось выше), что обеспечивает дисциплину обслуживания без ожидания.

Серверы системы представляются в виде систем массового обслуживания (СМО) с дисциплиной обслуживания PS (разделение процессора). Это соответствует особенностям общесистемного программного обеспечения, реализующего многозадачный режим работы, и высокопроизводительных вычислительных систем (IBM ES 9000, HP 9000, DEC), используемых в качестве серверов [6].

Маршрут передачи информации от пользователя к серверу, от сервера к серверу и обратно, от сервера к соответствующему пользователю описывается стохастической неразложимой матрицей

, где k- номер пользователя

(группы пользователей и, соответственно, типа сообщения) системы правовой информации, P_ij(k) — вероятность перехода из i-го узла по окончании обслуживания в j-й узел сообщения k-го типа [5]. Предполагается, что обслуживание в j-м узле сети происходит по экспоненциальному закону.

В сделанных предположениях указанная ЗСеМО удовлетворяет требованиям теоремы ВСМР [6,7], что позволяет получить основные характеристики сети (например, стационарное распределение вероятностей состояний сети) в конечном мультипликативном виде.

Стационарная вероятность состояния описанной выше сети представляется в общем виде следующим известным выражением [6, 7]:

где D - область допустимых состояний ЗСеМО; n - число конечных источников в ЗСеМО, m - число узлов СМО в ЗСеМО; p_j (k_j) - сомножитель мультипликативной формы, соответствующий j-му конечному источнику, генерирующему одновременно k_j запросов, k_j = 0, …, N_j, N_j - емкость j-го конечного источника, j' = 1, …, n, q_i (g_i) - сомножитель мультипликативной формы, соответствующий i-му узлу СМО; g_i = (g_i1, …, g_in) - состояние i-го узла, g_ij - число требований из j-го источника в i-м узле, j = 1, …, n, i = 1, …, т; f (l, P_k) - сомножитель мультипликативной формы, соответствующий центру IS сети передачи данных в ЗСеМО; l = (l₁, …, l_n - состояние центра IS, l_j - число требований из j-го источника на передаче в центре IS, j' = 1, …, n; G - нормировочная константа, определяемая из условия нормировки.

Указанная мультипликативная форма позволяет эффективно осуществить расчет средних характеристик РАСИПО. При этом для расчета могут быть использованы результаты, приведенные в источнике [6].

Как уже отмечалось выше, для более тонкого анализа работы системы и отдельных ее элементов целесообразно строить уточненные модели отдельных компонентов системы (подсистем). В данном случае будем рассматривать наиболее распространенную подсистему, где абонентские ЭВМ соединены с сервером в виде локальной вычислительной сети (используется стандарт IEEE 802.3). Будем полагать, что сервер обслуживает только подключенных к нему абонентов. При этом вычислительная сеть может быть представлена как многоканальная замкнутая двухфазная система массового обслуживания и ее структура может быть преобразована к виду, приведенному на рис. 3, что в общем является частным случаем структуры, показанной на рис. 2. Особенностью данной подсистемы является наличие конкуренции между сообщениями за право передачи по каналу связи (это соответствует особенностям стандарта IEEE 802.3).

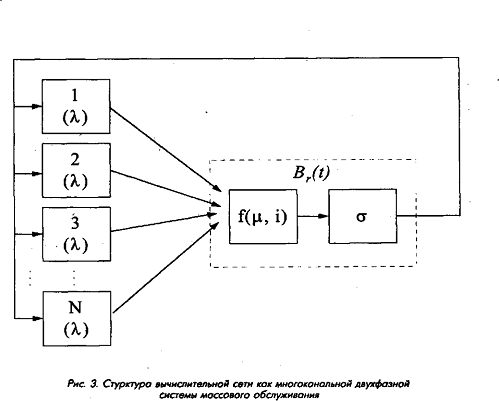
На первой фазе находятся ТУ приборов (источников), соответствующих станциям сети. После обработки сообщения на соответствующем ему приборе первой фазы оно поступает на прибор второй фазы СМО (на рис. 3 отмечен пунктиром; этому прибору соответствует канал передачи данных). После обслуживания на второй фазе каждое сообщение поступает на соответствующий прибор первой фазы системы. Считаем, что все приборы первой фазы одинаковы и длительность обслуживания сообщения на каждом приборе имеет экспоненциальное распределение с параметром X.

Отличительной особенностью СМО является зависимость длительности обслуживания на второй фазе от числа сообщений в очереди перед ней. Эта зависимость обусловлена процедурой состязаний между находящимися в очереди сообщениями за право обслуживания. Таким образом, длительность обслуживания реально складывается из длительности состязания и длительности передачи сообщения по каналу связи. Функцию распределения длительности обслуживания на второй фазе СМО обозначим через В (t, r), где r - число сообщений в очереди.

Под состоянием системы в момент t будем понимать число сообщений в очереди перед второй фазой.

Рассматривая систему в моменты окончания обслуживания на второй фазе, можно построить конечную вложенную цепь Маркова, которая будет в данном случае регулярной. Пусть p_i - стационарная вероятность того, что система находится в состоянии i.

Вероятности p_i связаны системой уравнений:

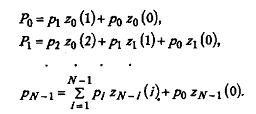
Здесь z_k (r) - вероятность поступления в очередь k новых сообщений за время разрешения конфликта между r сообщениями и передачей одного из них (kN-r).

Поскольку станции сети работают независимо (приборы первой фазы), то имеем:

где q_r - вероятность поступления сообщения с прибора первой фазы при наличии в очереди r сообщений - вычисляется по формуле

Здесь функция распределения длительности периода состояния и передачи сообщения при наличии в очереди г сообщений - В (t, r) - зависит от способа разрешения конфликта и может быть определена, например, из источника [9].

Приведенные соотношения позволяют проводить анализ системы в общем случае с позиции пользователя, т.е. определять такие характеристики, как время ожидания в очереди, вероятности состояний и т.д.

Часто необходимо оценивать эффективность использования канала. Для этого предлагается уточнить ранее приведенную модель и ввести третью фазу обслуживания путем разбиения на две части второй фазы в предыдущей модели (см. рис. 3). При этом новая вторая фаза соответствует задержке на процедуру состязания, а третья - задержке на передачу сообщения.

Будем считать, что длительности обслуживания на второй и третьей фазах системы есть случайные величины с экспоненциальным распределением параметрами µ и σ для каждой фазы соответственно.

Интенсивность поступления сообщений на третью фазу зависит от числа сообщений i, имеющихся на второй фазе. Поскольку каждое сообщение может поступить на обслуживание только тогда, когда в течение времени T не поступит других сообщений (не произойдет столкновения), вероятность чего равна

, то интенсивность поступлений на обслуживание определяется выражением

Под состоянием системы в данном случае будем понимать пару (i, j), где i' - состояние обслуживающего прибора третьей фазы (i = 0 - прибор свободен, j = 1 - прибор занят); j = 1, N - число сообщений на второй фазе, т.е. число станций, пытающихся занять канал.

Пусть p_ij - стационарная вероятность пребывания системы в состоянии (i, j). Система уравнений для нахождения p_ij имеет для состояний типа (1, i) (i = 1, …, N-1) следующий вид:

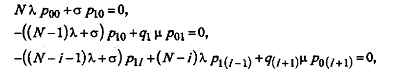
а для состояний типа (0, i) (i=1, …, N)

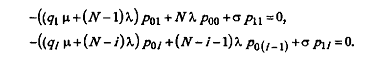
При решении системы необходимо воспользоваться условием нормировки

Зная вероятности состояний системы, можно определить такие ее характеристики, как среднее число сообщений в системе и коэффициент использования канала.

По результатам расчетов коэффициента использования канала на ЭВМ были построены графические зависимости, представленные на рис. 4.

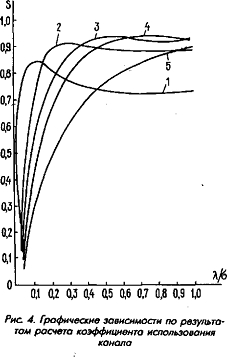
Зависимость коэффициента использования канала от загрузки.

Кривая 1: N = 20; кривая 2: N = 10; кривая 3: N = 7; кривая 4: N = 5; кривая 5:

N = 3; Т = 0,005 мс; µ = 20.

Совокупность "грубых" и "тонких" моделей позволяет проводить как качественный анализ системы в целом, так и уточненный анализ отдельных ее подсистем. Предложенные математические модели дают возможность получить основные характеристики сети в удобном для практического применения виде.

1. Киселев Б.В., Хургин В.М. Информационные проблемы в правовой сфере//Вестник РОИВТ, ВИМИ, 1994. Вып. 1-2.

2. Хургин В.М. Информационное взаимодействие с региональными органами власти//Вестник РОИВТ, ВИМИ. 1994. Вып. 6.

3. Бертсекас Д., Галлагер Р. Сети передачи данных//М.: Мир, 1989.

4. Саксонов Е.А. Исследование многоканальной замкнутой циклической системы массового обслуживания//Автоматика и телемеханика, 1979, № 12.

5. Фрэнк Г., Фриш И. Сети, связь и потоки//М.: Связь, 1978.

6. Жожикашвили В.А., Вишневский В.М. Сети массового обслуживания. Теория и применение в сетях ЭВМ//М.: Радио и связь, 1988.

7. Уолрэнл А. Введение в теорию сетей массового обслуживания//М.: Мир, 1993.

8. Яшков С.Ф. Анализ очередей в ЭВМ//М.: Радио и связь, 1989.

9. Никитин Н.М., Окунев С.Л., Саксонов Е.А. Алгоритм разрешения конфликтов в локальной сети со случайным множественным доступом//Автоматика и вычислительная техника, 1985, № 5.

___________________________________________________________________

Саксонов Е.А. - доктор технических наук, профессор

Хургин В.М. - кандидат технических наук

---

&copy Информационное общество, 1996, вып. 5, с. 29-36.