Параллельные методы вычислений в задачах радиационного переноса излучения с учетом его взаимодействия с веществом
Долголева Г.В.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 93-012-1037).

Описываются возможные подходы распараллеливания в методике, построенной на расщеплении по физическим процессам. Практически распараллеливание было проведено в аппаратной среде, состоящей из пяти 77М-100. Распараллеливание проводилось в рамках программы SND.

В отличие от обычных подходов распараллеливания численных методов по геометрическим характеристикам ниже рассматривается распараллеливание численных методов по физическим процессам. При рассмотрении такого подхода необходимо иметь характерный пример методики, описывающей набор различных физических процессов. В качестве такого примера выбрана методика SND [1 ], по которой рассчитываются следующие физические процессы:

движение системы в двухтемпературном приближении с учетом физической вязкости;

перенос тепла ионами и электронами с ограничением диффузионного потока;

поглощение и перенос лазерной энергии и рентгеновского излучения;

перенос излучения и взаимодействие его с веществом в приближении спектральной неравновесной диффузии.

Неравновесность среды рассчитывается по системе уравнений ионизационной кинетики.

Численный исходный последовательный алгоритм для решения названной выше системы построен с учетом расщепления по физическим процессам [2 ].

Запишем систему уравнений в частных производных в операторной форме

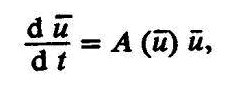
где

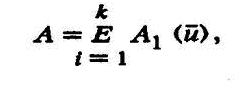
А — матрица, описывающая тот или иной физический процесс — i;

к — количество рассматриваемых физических процессов;

u = u_1, u_2, ...,u_m — вектор решения.

Разностным аналогом этой системы является система

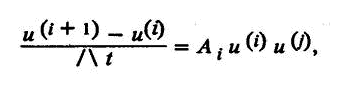
где a, b = n, n+1.

Для каждого физического процесса а и b свои, в зависимости от явности или неявности конкретной разностной схемы.

Метод расщепления — это разбиение исходной системы на к (количество рассматриваемых физических) подсистем

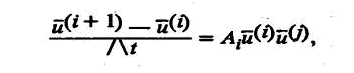
где i = 1 (i) = n, при i = k (i + 1) = n + 1.

Чтобы приступить к расчету (i)-этапа, мы должны знать значения искомого решения на предыдущем (i—1) этапе. В этой последовательности действий и состоит главная сложность распараллеливания по физическим процессам.

Наиболее простой подход — значения рассчитываемых величин по всем физическим процессам, которые учитываются в отдельности, определять по состоянию их в предыдущем слое по времени.

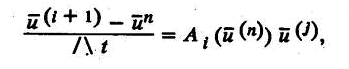
где

j=n, (i+1).

Окончательно полагаем

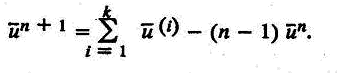
Просуммировав подсистемы (4) по всем i с учетом (5), мы действительно получим систему уравнений (2).

В этом случае возникают свои осложнения:

во-первых, такой подход существенно изменяет вычислительный алгоритм и снижает аппроксимацию разностной схемы;

во-вторых, время счета того или иного физического процесса очень различно. Для примера приведем разницу времен для конкретной задачи, о которой будет сказано ниже. Отличие времени счета уравнений газодинамики от времени счета неравновесной диффузии доходит до двух порядков. Это максимальное отличие для данной задачи. Времена счета других процессов также отличаются друг от друга. Причем эти отличия непостоянны: они меняются не только от задачи к задаче, но и внутри одной задачи от одного счетного шага к другому. И совсем не простая задача при таком подходе — балансировка (распределение) физических процессов по отдельным процессорам с их максимальной загрузкой.

Рассмотрим пример иного подхода к распараллеливанию исходя из конкретной системы дифференциальных уравнений, заложенной в методике SND. Он строится, как указывалось выше, с учетом специфики построения исходного алгоритма для последовательного счета:

тот или иной физический процесс пересчитывает вектор u неполностью. Например, по уравнениям газодинамики мы пересчитываем скорость, плотность, энергию, но не пересчитываем плотность излучения, концентрации веществ. Самая первая задача (глобальная) в нашем подходе — это выделение тех физических процессов, которые можно рассчитывать независимо друг от друга, и размещение их на различные процессоры для одновременного счета;

внутри такого глобального распараллеливания по физическим процессам постараться распараллелить времяемкие процессы.

В качестве примера реализации такого подхода приведем результаты счета двух задач. Расчеты проводились на ТТМ-100 и в аппаратной среде из пяти ТТМ-100.

Рассматривались следующие задачи:

расчет тепловой волны с ионизацией частиц плазмы электронным ударом. Рассчитываются уравнение для внутренней энергии с учетом электронной тепло­проводности и уравнения ионизационной кинетики. При определенных значениях коэффициентов, начальных и граничных условиях задача имеет аналитическое решение. Это решение можно получить численно, если количество концентраций равно i, или, что эквивалентно, количество рассчитываемых уравнений в системе ионизационной кинетики бесконечно. Проводились расчеты с i - 10, 20, 40. В таблице они имеют мнемонические названия KNI10, KNI20, KNI40 соответственно. Для этих задач характерно обращение матриц порядка 10, 20, 40 соответственно на каждом временном шаге, в каждой точке по пространству и на итерациях, что определяет большой объем вычислительной работы. В расчетах было выбрано 50 точек по пространству. Число временных шагов в первой задаче 205, во второй — 338, в третьей — 292;

расчет сжатия плоской мишени, облучаемой лазерным излучением. Рас­считывается движение системы, перенос тепла электронами и ионами, поглощение и перенос лазерной энергии, перенос излучения и взаимодействие излучения с веществом, неравновесность среды в приближении среднего иона. Перенос излу­чения рассчитывается в спектральном приближении. В таблице эта задача имеет мнемоническое название LAZR. В задаче 60 точек по пространству, 80 групп по спектру, 599 временных шагов.

Эффективность загрузки находится на уровне 50 %. Это мало по сравнению с эффективностью, получаемой при распараллеливании по геометрии. В этих случаях ее можно довести до 98 % для определенного класса задач (например, задачи аэродинамики). Для последней из рассмотренных выше задач приведено две цифры. Это результат работы по дополнительному распараллеливанию внутрифизических процессов, который показывает, что есть возможность значительно улучшить представленные характеристики.

Примечания: 1. Четвертый столбец – ускорение: во сколько раз на пяти платах задача считается быстрее, чем на одном. 2. К_эф – эффективность загрузки пяти процессов, вычисленная на формуле К_эф = t₁ / (t_N * N), где t₁ – время счета задачи на одном процессоре; t_N – время счета задачи на N процессорах; N – число процессоров.

Приведены первые результаты работы по распараллеливанию конкретной методики с ее организационной структурой уже.отработанными численными методами. При проведении работы по распараллеливанию, выяснилось также, что неплохо бы изменить устоявшуюся в методике структуру двумерных массивов, используемые численные методы.

Это дело будущего.

ЛИТЕРАТУРА

1. Долголева Г. В. Методика расчета движения двухтемпературного излучающего газа (CHD) //ВАНТ. Сер. Методики и программы численного решения задач математической физики, 1983, вып. 2 (13), с. 29—33.

2. Я н е н к о Н. Н. Метод дробных шагов решения многомерных задач математической физики. Новосибирск: Наука, 1987.