Биоинформатика
Чернавский Д.С.

Даны основные понятия и определения в области биоинформатики — раздела информатики, учитывающего особенности сбора, хранения, обработки и использования информации в биологических системах. При этом возникли следующие проблемы, которые в традиционной информатике детально не исследовались: генерация ценной информации и спонтанное возникновение цели. Эти проблемы связаны с возникновением жизни, единого биологического кода и биологической асимметрии.

Процессы сбора информации, ее хранения, передачи и переработки исследуются давно и составляют предмет науки информатики.

В живой природе упомянутые процессы тоже играют роль, но помимо них в биологии встают и решаются дополнительные вопросы, а именнно: как возникает информация, какова ее ценность и каковы механизмы реализации ценной информации? Эти вопросы определяют специфику биоинформатики и ее методов исследования. В традиционной информатике внимание акцентируется на проблемах технического характера. Вопрос о ценности информации решался также в прикладном аспекте. Принималось, что информация используется для достижения определенной цели, которая и определяет ее ценность.

В работах Бенгарта [1] и Харкевича [2] была предложена мера ценности в форме

где V_i — ценность данной (i-й) информации; Рⁱⁿ и P_i^fin — вероятность достижения цели до и после получения информации. Эта мера удобна, когда вероятность Рⁱⁿ мала.. В работах Стратоновича [3] предлагалась другая мера, удобная в случае, когда цель наверняка достижима (Pⁱⁿ = 1), но пути ее достижения требуют различных затрат (времени, средств и др.). В обоих случаях считалось, что цель определена, т. е. задается кем-то, и вопрос о том, как цель формируется, не обсуждался.

В биологии, особенно в проблемах возникновения жизни и биологической эволюции, встает вопрос о том, как возникает цель и возможно ли это возникновение без вмешательства свыше. Иными словами, мы сталкиваемся с вопросом о том, какова цель жизни. Ясно, что он имеет фундаментальный и даже методологический характер.

В этой связи вопрос о том, что такое информация, требует более точного Определения.

Дело в том, что существуют два разных определения.

Согласно Кастлеру [4 ], информация есть запомненный выбор одного варианта из N возможных. Количество информации при этом равно: I = ΣP_i,-log₂ P_i.; i =1,2, 3,... N,P_i — вероятность выбора i-го варианта a priori. В простейшем случае, когда P₁ = Р₂ =... = Р = 1/N, I=log₂ N.

Информация в смысле Бриллюэна отличается тем, что не содержит условия "запоминания".

Первую называют также макроинформацией, а вторую — микроинформацией.

Условие "запоминания" играет очень важную роль: без него невозможны ни хранение, ни обработка информации. Во всех реальных случаях мы практически имеем дело с макроинформацией [5 ].

Количественная разница между макро- и микроинформациями также очень велика. Микроинформация связана с физической энтропией простым соотношением: /_микр0 = ∆S/k In2, где ∆S — изменение физической энтропии, к — постоянная Больцмана. Макроинформация с энтропией не связана, и изменения ее много меньше изменений энтропии: ∆I_макро<<∆S/kIп2. Причина этого в том, что запоминание — процесс макроскопический и диссипативный. Он сопровождается большим изменением физической энтропии. Микроинформация обсуждается преимущественно в теорфизических спекуляциях по поводу энтропии, к реальной информатике она отношения не имеет.

Мы остановились на этом вопросе потому, что процесс "запоминания" в биологии осуществляется на молекулярном уровне, и поэтому разделение информации на макро и микро требует особого внимания.

Для демонстрации особенностей биоинформатики рассмотрим ряд примеров.

Генерация ценной информации обсуждалась в связи с проблемой возникновения единого генетического кода [6] (возникновения жизни), появлением биологической асимметрии [7] и возникновением новых видов [8, 9]. В первом случае речь идет о выборе из многих вариантов (полное число возможных генетических видов велико: N«20>>1). В двух других случаях речь идет о выборе одного варианта из двух (N= 2). В [6, 10] была предложена математическая модель, описывающая процесс генерации ценной информации, которая имеет вид:

Начальные условия задавались в симметричной форме: при t = 0; и₁ = u₂ =^UN

Эволюцию системы, описываемой моделью (2), можно разделить на три этапа [10].

Первый этап — разрушение исходного симметричного соотношения (в силу его неустойчивости) и образование "чистых" кластеров (в которых находятся преимущественно элементы какого-либо одного типа) и границ между ними, что показано на рис. 1, а, где представлен случай N=3.

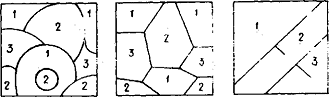
Рис. 1. Этапы процессы генерации ценной информации; выбор единого биологического кода

Второй этап — выпрямление границ, образование картины типа паркета и медленная эволюция, в результате которой мелкие кластеры исчезают, а крупные увеличиваются (рис. 1, б).

Третий этап — образование чистого состояния, в котором все пространство занято одним кластером (рис. 1, в).

Предсказать заранее, какое именно состояние окажется доминирующим, невозможно, ибо уравнение (2) и начальные условия симметричны, а на промежуточных этапах имеет место хаотическое поведение.

Отметим, что эти свойства сохраняются, если исходная симметрия нарушена, но не сильно (члены авторепродукции и взаимодействия неодинаковы, т. е. при них стоят коэффициенты b_i и c_ij порядка единицы).

В рамках модели оказалось возможным следующее.

Сформулировать основную цель носителей информации (эта цель — сохранение собственной информации).

Проследить процесс генерации ценной информации, т. е. процесс выбора одного из N возможных чистых состояний.

Подчеркнем принципиальное отличие выбора от отбора. При отборе предполагается, что один из вариантов обладает преимуществом и именно от остается в результате отбора. При выборе варианты a priori равноправны (или почти равноправны) и выбранный случайно вариант необязательно является наилучшим. Для осуществления выбора необходимо наличие нейтральной информации (чтобы было из чего выбирать). Отсюда видна связь генерации ценной информации с нейтралистской теорией эволюции.

В биологической эволюции участвуют выбор и отбор. Первый важен на дивергентных стадиях эволюции и протекает быстро, второй — на конвергентных стадиях и осуществляется медленно.

Определить ценность информации i-го типа на каждом этапе. При этом выяснилось, что на первых этапах ценность любой информации близка к нулю, но возрастает при переходе от второго (хаотического) этапа к третьему (динамическому). Этот момент можно назвать моментом генерации ценной информации.

Наиболее ценной оказывается при этом информация, соответствующая чистому кластеру, вытеснившему других конкурентов.

Подчеркнем наличие квазихаотического этапа — очень важное и необходимое свойство любой системы, в которой происходит генерация информации. С другой стороны, квазихаос (или, что то же, повышение вариабельности) является необходимым следствием прохождения через бифуркацию, когда система теряет устойчивость. Поэтому вариабельность играет особо важную роль в биоинформатике как в фундаментальном, так и в прикладном аспектах.

Так, повышение вариабельности является ранним и чувствительным тестом приближающейся опасности и в этом аспекте может использоваться в экологии [11,12].

Момент, когда вариабельность достигает максимума, является тестом для определения времени принятия решения [10 ], что важно не только в биологии.

Модель типа (2) использовалась не только в биологии. Эволюция языков подчиняется тем же правилам. В последнее время эта модель использовалась для описания формирования общественного мнения [13 ] и "моды" на потребительском рынке [14].

Таким образом, модель (2) описывает широкий круг явлений — от возникновения жизни в первичном бульоне до процессов в человеческом обществе. В последнем генерация ценной информации тесно переплетается с проблемами принятия решения и творчества. Действительно, принятие решения в условиях недостатка информации (а только в этих условиях проблема нетривиальна) — пример выбора определенного варианта, т. е. генерация ценной информации.

Сказанное выше о выборе момента генерации информации относится также и к моменту принятия решения. То же можно сказать и об акте творчества.

Проблема переработки информации (извлечение из нее ценной информации) традиционно входила в раздел информатики, именуемый теорией распознавания образа. В последнее время появилось новое направление — нейрокомпьютинг. Первая часть слова "нейро" оправдана исторически и означает, что первоначально нейропроцессор рассматривался как модель реальной нейросети. При этом внимание акцентировалось не на свойствах элементов сети — "нейронов" (для их моделирования выбирался простейший вариант — бистабильный элемент), а на свойствах связи между ними.

Принципиальную роль сыграло введение "обучаемых" связей, свойства которых могут изменяться в процессе работы.

Идеи оказались плодотворными в прикладном аспекте, и в результате сейчас нейрокомпьютинг — направление компьютерной науки (computer science), практически не связанное с нейрофизиологией.

В рамках этого направления возникли новые понятия и принципы конструкции нейрокомпьютеров (парадигмы). Напомним их кратко.

Кроме "обучения связей" возникли следующие понятия:

"внимание" — перераспределение порогов возбуждения элементов, которое ускоряет процесс узнавания определенных образов. С помощью "внимания" можно компенсировать дефекты процесса обучения, однако если "внимание" распределено неадекватно, то могут возникнуть ошибки распознавания;

"подтверждение" — повторное узнавание, возможно с некоторой модификацией поступающей информации. При этом результаты каждого узнавания запоминаются и затем сопоставляются друг с другом;

"локализация образа" — процесс, в результате которого каждый образ предстает в виде одного определенного возбужденного элемента, что облегчает распределение "внимания".

Ради краткости мы не обсуждали ряд других парадигм, касающихся контрастности образа, очищения от шумов и др.

Несколько слов о конструкциях нейрокомпьютеров.

Каждый процессор представляет собой пластину, в которой размещены элементы, связанные друг с другом большим количеством обучаемых связей. Число связей, приходящихся на каждый элемент, достаточно велико (хотя и меньше максимального числа n — 1, где n — число элементов в пластине). Сигналы, передаваемые по связям, могут иметь как возбуждающий, так и тормозящий характер. На вход каждого элемента подводятся связи от другой пластины либо извне, число их мало по сравнению с числом связей внутри пластины. Кроме того, к каждому элементу подводится связь, регулирующая порог восприятия ("распределение внимания").

Из изложенного следует, что пластинчатая (двумерная) конструкция нейро-процессора играет принципиальную роль. Именно она обеспечивает сильные связи внутри процессора и одновременно доступность элементов для внешних и межпластинчатых связей.

Для реализации парадигм "подтверждение" и "локализация" необходимо использовать несколько связанных друг с другом пластин.

До недавнего времени упомянутые результаты нейрокомпьютинга практически не использовались в нейрофизиологии по причинам взаимонепонимания.

Задача биоинформатики — использовать достижения нейрокомпьютинга для интерпретации богатейшего фактического материала, накопленного в нейрофизиологии.

Такая попытка была сделана в работах [15, 16] с целью понять механизм терапевтического эффекта сравнительно слабых воздействий, в частности пунктур-ной терапии.

На основе теории распознавания были сформулированы условия, которым должна удовлетворять аутодиагностическая система (АДС) человека. Сопоставление с нейрофизиологическими данными (о биохимии, морфологии и функциях) дало основание утверждать, что роль АДС выполняет часть центральной нервной системы, составляющая серое вещество спинного мозга и известная в нейрофизиологии под названием "пластины Рекседа". К ним поступают сигналы от внутренних органов и биологически активных точек кожи. Последние возникают при пунктурном воздействии и могут играть корректирующую роль в случае, если АДС как распознающая система работает не вполне адекватно.

Коррекция диагноза (в данном случае аутодиагноза) мобилизует защитные силы организма, что и обеспечивает терапевтический эффект. Аналогична ситуация в медицине: ошибка в диагнозе должна быть исправлена, только в этом случае возможна адекватная терапия.

Третий пример касается проблемы использования генетической информации при развитии организма (т. е. в онтогенезе). При этом исходное состояние сравнительно просто (например, оплодотворенная яйцеклетка). Конечное состояние — похожий на своих родителей сложный организм. На промежуточных этапах организм приобретает формы, характерные для видов-предшественников, а в определенные моменты ведет себя как хаотическая система [17]. Известно утверждение: онтогенез есть повторение филогенеза. Смысл последнего мы обсудим ниже. До сих пор идет дискуссия по поводу того, какой из факторов важнее — генетическая информация или самоорганизация. Более корректно вопрос можно поставить в следующей форме: каков механизм использования генетической информации в процессе развития организма?

Для исследования онтогенеза часто используется более простой процесс — образование псевдоплазмодия в колонии социальных амеб Dictiostellium discoideum. Процесс состоит из ряда стадий, схематически приведенных на рис. 2. Исходное состояние — колония одноклеточных организмов, существующих

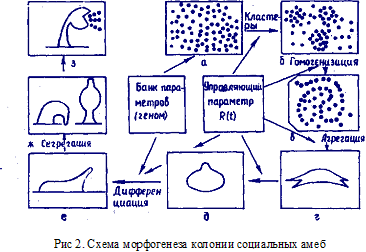
независимо друг от друга (рис. 2, а). При исчерпании запасов питания амебы собираются в кластеры (рис. 2, б), затем снова рассыпаются и образуют центростремительные струи [спиральные или радиальные (рис. 2, в) ]. Агрегация заканчивается образованием псевдоплазмодия (рис. 2, г, д), в котором происходит дифференциация клеток на пристеблевые и приспоровые. Псевдоплазмодий движется по поверхности и ведет себя подобно целому организму (рис. 2, е). Затем дифференцированные клетки разделяются в пространстве (сегрегация), пристеблевые клетки сначала собираются в "голове", последняя прикрепляется к подложке, и в противоположном конце образуется мешок со спорами (рис. 2, е, ж). На этом процесс образования организма заканчивается, ибо последующие процессы тривиальны: мешок лопается, споры разносятся ветром (рис. 2, з), а вся оставшаяся часть отмирает. Процесс хорошо изучен экспериментально, более того, построены математические модели, описывающие отдельные стадии в соответствии с опытными данными.

М од ель, описывающая процесс в целом, была предложена и исследована в работе [18 ]. Приводить ее здесь не будем во избежание загромождения. Обсудим лишь ее структуру, она проста. Модель содержит шесть уравнении, но в каждый момент реально работает лишь один блок из двух-трех уравнений. Имеется седьмое простое уравнение для "управляющего параметра"7? (О, которым в данном процессе является запас питательных веществ. Оно описывает медленное монотонное убывание величины R (t). Величина R(t ) входит во все уравнения как бифуркационный параметр. Переход от одной стадии к другой (переключение) совершается в момент, когда параметр R достигает бифуркационного значения.

Таким образом, в модели на конкретном примере реализуется принцип параметрической регуляции морфогенеза, сформулированный в работах [9,17 ].

Роль генома сводится к следующему.

Геном определяет параметры системы (т. е. белковый состав) в начальный момент развития. Этот состав практически не меняется вплоть до момента дифференциации. Таким образом, все начальные стадии протекают без регулирующего воздействия со стороны генома. При дифференциации экспрессируются гены и синтезируются белки, характерные для приспоровых и пристеблевых клеток, т. е. геном выдает информацию о параметрах, необходимых для последующего развития. Дальнейшие процессы протекают также без вмешательства генома.

Иными словами, в момент, когда система должна сделать выбор (принять решение), она обращается к геному и последний выдает информацию, предопределяющую выбор. Таким образом, в процессе морфогенеза ценная информация не генерируется, но рецептируется из генома в нужный момент и в нужном количестве. Определение "нужного момента", а также процессы реализации информации протекают самопроизвольно и в генетическом контроле не нуждаются.

Из модели ясно, в чем отличие онтогенеза от филогенеза. В последнем присутствует акт генерации ценной информации. Выбор был запомнен и сохранен в геноме. В результате в онтогенезе акт генерации ценной информации заменен актом рецепции из генома.

Приведенные примеры не -исчерпывают всех проблем биоинформатики. Например, в статье не рассматривались вопросы биомолекулярного компьютинга, которому посвящена обширная литература [19]. Однако приведенного достаточно для того, чтобы подвести следующий итог.

Биоинформатика — научное направление, цель которого связать информатику и теоретическую биологию.

С одной стороны, биоинформатика решает проблемы, которые в биологии поставлены давно, а именно: генерация ценной информации и ее использование. С другой стороны, биоинформатика помогает решать биологические проблемы, используя достижения технической информатики.

Методическая особенность биоинформатики в том, что она опирается на математические модели процессов генерации и реализации информации.

ЛИТЕРАТУРА

1.Бонгарт М. М. Проблема узнавания. М.: Наука, 1967.

2. X а р к е в и ч А. А. Теория информатики. Опознавание образов. М.: Наука, 1973.

3. Стратонович Р. Л. Теория информации. М.: Сов. радио, 1975.

4. Кастлер Г. Возникновение биологической информации. М.: Мир, 1967. (Quastler Н., The Emergence of Biological Organization, Yale Univ. Press, N. Y., 1964).

5. Volkenstein M. V., Chernavskii D. S. Evolution and Value of Information.— In: Self-Organization / Ed. V. I. Krinsky, Springer-Verlag, Berlin, Heidelberg, N. Y., Tokyo, 1984.

6. Chernavskaya N. M., Chernavskii D. S. Some Theoretical Aspects of the Problem of life Origi // J. Theor. Biol. 1975. Y. 53. P. 13—20.

7. Романовский Ю. M„ Степанова H. В., Чернявский Д. С. математическое моделирование в биофизикеЛ!.: Наука, 1975.

8. С h е г па v s к а у а N. М., С h е г п a v s к i 1 D. S. On the Problem of the Origin of Biological Information. — In: Molecular Evolution and Protoblology / Ed. K. Matsuno, Plenum Press, N. Y., London, 1984. P. 365—374.

9. Романовский Ю. M., Степанова H. В., Чернавский Д. С. Математическая биофизика. М., 1984.

10. Чернавский Д. С. Синергетика и информация. М.: Знание, 1990.

11. Веселова Т. В., ВеселовскийВ. А., ВласенкоВ. В., МацкавскийВ.И., Пеньков Ф. М., Чернавский Д. С. Вариабельность как тест перехода в состояние стресса в условиях интоксикации / / Физиология растений. 1990. Т. 37. № 4. С. 733—739.

12. Столяров М. И., Чернавский Д. С. О биологической вариабельности//Биофизика.
1992. Т. 37. С. 363—376.

13. Weidlich W. Physics and Social Science — The Approach to Synergetics, Phys. Rep., 1991.

14. Экономика как развивающаяся система: Сб. статей // Университет Санта-Фе, 1988. 15.Чернавский Д. С, Карп В. П., Родштат И. В. О нейрофизиологическом механизме КВЧ-пунктурной терапии. Препринт ФИАН, 1991, № 150.

15. Чернавский Д. С, Карп В. П., Родштат И. В. Об аутодиагностической системе человека и ее роли при пунктурной терапии // Радиофизика (в печати).

16. Белоусов Л. В., Чернавский Д. С, Соланин Г. И. Приложения синергетики к онтогенезу (о параметрическом управлении развитием) //Онтогенез. 1985. Т. 16. №3. С. 213-228.

17. БелинцевБ. Н., Чернавский Д. С, ВолькенштейнМ. В. физико-математическая модель коллективного развития Dictiost. disc. // Молекулярная биология. 1992. Т. 26. № 2. С. 328—341. 26. №2. С. 328—341.

18. Ram Ы diN. С, Cherna vskiiD. S., S a n d 1 е г Yu. M. Towards a Biomolecular Computer // Jour. Mol. Electr., 1991. V. 7.1, П. P. 115—125.

_________________________________

Д. С. Чернавский - д-р физ.-мат. наук