Увеличение скорости обработки информации с помощью алгоритма Уитни методом введения стандартных ситуаций
Архангельский А.Б., Панкратов М.Г.

Рассмотрены методы повышения скорости обработки информации с помощью алгоритма Уитни. Представлены как математические, так и эвристический методы. Приведены примеры.

Одним из узких мест в автоматизированном проектировании изделий микроэлектроники является технологическая подготовка производства, включающая в себя подсистемы подготовки управляющих программ оборудования подготовки фотошаблонов. Это обусловлено как специфическими особенностями самих установок, так и сложностью алгоритмов вычислительной геометрии, лежащих в основе пакетов технологических постпроцессоров. Использование новых физических принципов при проектировании кристаллов БИС и СБИС из инструментальных средств автоматизированного проектирования оставляет конструктору-технологу только инвариантные графические подсистемы подготовки топологий, не обеспеченные библиотеками элементов и методиками расчета параметров, и подготовка управляющих программ для технологического оборудования в производстве фотошаблонов неадекватно поддерживается стандартными системами проектирования. Таким образом, задача разработки высокопроизводительных постпроцессоров, настраиваемых на различные технологии, с хорошим контролем всех этапов проектирования представляется нам актуальной.

В настоящее время в производстве БИС и СБИС для изготовления фотошаблонов широко применяются генераторы изображений, требующие покрытия лэйау-тов специальными геометрическими фигурами. Задача оптимального покрытия лэйаутов не является NP-полной, и эвристическим алгоритмам работы подсистем покрытий топологий кристалла для генераторов изображений посвящено большое число статей и монографий. Наиболее детально исследован случай, когда экспозиции фотонаборной установки представляют собой прямоугольники и топология кристалла является областью с кусочно-линейной границей. Здесь эталонным алгоритмом является фронтальный, имеющий сложность n*log(n) - минимальную среди всех известных алгоритмов; здесь и ниже п - число угловых точек границы. Сразу же отметим, что фронтальный алгоритм требует специальной сортировки данных, что не позволяет понизить его сложность.

Применение микро- и мини-машин в задачах автоматизированного проектирования позволило конструктору получить в личное пользование все ресурсы ЭВМ и удобные инвариантные графические системы, составляющие конкуренцию АРМам (например, AutoCAD, PCAD и др.). Однако технологические системы разработаны в этом классе машин существенно слабее, так как они требуют большой памяти и высокого быстродействия. Для работы в ограниченных ресурсах должны применяться, новые алгоритмы с использованием разделения функций системы. Заметим, что с точки зрения математики речь идет о покрытии произвольного плоского открытого множества прямоугольными областями. Наиболее известным и алгоритмизуемым результатом в-этом вопросе является теорема Уитни о покрытии, используемая ранее только как инструмент для доказательства существования гладкого продолжения функций. Здесь приводится описание технологического процессора, реализованного на микроЭВМ с использованием специальной рекурсивной реализации алгоритма Уитни.

Суть покрытия Уитни состоит в следующем. Рассмотрим прямоугольник со сторонами, параллельными оям координат, и содержащим границу топологии кристалла. Разобьем его на четыре пересекающихся только по границе равных прямоугольника, полученных из исходного гомотетией и сдвигом. Для каждого из полученных прямоугольников проверим истинность следующих выражений: прямоугольник не пересекается с границей топологии и лежит вне лэйаута, прямоугольник не пересекается с границей топологии и лежит внутри лэйаута. Если хотя бы одно из этих выражений является истинным, соответствующий прямоугольник не включается или включается в число экспозиций. Если оба выражения ложны, данный прямоугольник обрабатывается так же, как исходный. Процесс повторяется до тех пор, пока размеры рассматриваемых прямоугольников превышают технологические возможности фотонаборной установки. Легко видеть, что сложность описанного алгоритма составляет п. Действительно, при фиксированном исходном прямоугольнике число его разбиений на более мелкие числа фиксированное, хотя и большое и не зависит от числа угловых точек границы лэйаута. Для проверки условия "внутри-снаружи" необходим один просмотр угловых точек границы. Более детальный анализ показывает, что число производимых элементарных операций пропорционально жордановой длине границы, умноженной на число угловых точек. Таким образом, теоретическая сложность алгоритма Уитни ниже сложности эталонного алгоритма.

Как уже отмечалось, число разбиений исходного прямоугольника фиксированно и является достаточно большим. Это обстоятельство не позволяет при рекордной сложности алгоритма достичь высокой скорости обработки информации. Использование алгоритма Уитни позволяет получить выигрыш во времени обработки при условии m < log(n), где m - число прямоугольников, покрывающих область определения лэйаута. В противном случае время обработки становится неприемлемо большим. Последнее обстоятельство показывает, что для увеличения скорости работы необходимо сократить число тестируемых прямоугольников.

Детальный анализ позволяет выделить следующие узкие места алгоритма Уитни. Во-первых, для каждого прямоугольника производятся вычисления, позволяющие решить проблему его расположения по отношению к лэйауту -"внутри-снаружи". Во-вторых, число тестируемых прямоугольников растет Обратно пропорционально расстоянию до границы топологии. Другими словами, алгоритм Уитни следует дополнить специальными скоростными методами покрытия в окрестности границы лэйаута и попытаться сократить вычисления расположения прямоугольников.

Рассмотрим сначала проблему "внутри-снаружи". Наиболее известным методом решения этой задачи является вычисление вращения поля векторов, выходящих из центра тестируемого прямоугольника, концы которых лежат на границе связного элемента топологии. Если вращение не равно нулю (при условии отсутствия пересечений прямоугольника с границей), тестируемый прямоугольник принадлежит лэйауту. Легко видеть, что векторные поля, построенные для двух прямоугольников с общей границей, гомотопны, если эти прямоугольники не пересекаются с границей топологии. Использование этого обстоятельства позволяет во многих случаях ограничиться вычислением пересечения тестируемого прямоугольника с границей топологии. Далее стандартные методы вычисления вращения требуют вычисления углов, т. е. применения тригонометрических функций. Заметим, что вращение описанного векторного поля равно индексу особой точки (центр тестируемого прямоугольника) по отношению к границе связного элемента лэйаута. Если граница является гладким многообразием, имеется простой метод вычисления индекса точки. Назовем пересечение границы с лучом, выпущенным из особой точки, положительным, если определитель матрицы, первая строка которой есть координаты направляющего вектора луча, вторая строка - координаты касательного вектора в точке пересечения луча с границей, - больше нуля, и назовем пересечение отрицательным, если соответствующий определитель меньше нуля. Хорошо известен следующий факт (см., например, [5]). Для почти каждого луча, выпущенного из особой точки, ее индекс с точностью до знака равен разности суммы положительных пересечений с границей и суммы отрицательных. Распространение гомотопией этого метода вычисления индекса на топологии, граница которых является кусочно-линейной, приводит к следующему алгоритму вычисления вращения векторного поля. Проведем из особой точки луч, для удобства вычислений параллельный осям координат. Когда луч не пересекает угловые точки границы, мы находимся в условиях гладкого многообразия. Отрезки, параллельные лучу, выбрасываются из рассмотрения. Бели же луч пересекает границу в угловой точке, вклад этого пересечения в индекс равен половине разности суммы положительных и суммы отрицательных пересечений с отрезками границы, составляющими угол. Более детальный анализ показывает, что вычисление определителей и пересечений с лучом можно заменить четырьмя неравенствами.

Проблема специализированного алгоритма в окрестности границы решается обработкой типичных ситуаций пересечений тестируемого прямоугольника с границей. Набор типичных ситуаций со специальными алгоритмами покрытий можно увеличивать до бесконечности. Включение нового случая равносильно дополнительной проверке условий. Ясно, что каждая проверка будет замедлять работу программы, поэтому существует набор, позволяющий на топологиях средней сложности добиться оптимальной скорости обработки. Теоретически этот набор вычислить очень сложно. Однако его можно определить экспериментально. Ниже мы представляем типичные ситуации, включение которых в алгоритм Уитни привело к увеличению'скорости обработки в сотни раз. Структура оптимального набора стандартных ситуаций нам неизвестна. Обработка типичных (стандартных) ситуаций реализована как закрашивание прямоугольных и треугольных фигур, поэтому в дальнейшем мы будем применять наряду с термином покрытие термин закрашивание.

Алгоритм, закрашивания прямоугольного треугольника выглядит следующим образом. Средние линии, параллельные катетам, делят треугольник на прямоугольник и два треугольника, гомотетичных исходному. Прямоугольник экспонируется, а к треугольникам применяется та же операция со средними линиями (рис. 1). Рекурсивная реализация этого алгоритма представлена ниже.

Перейдем теперь к рассмотрению стандартных ситуаций. Наиболее простой случай, когда квадрат пересекается одним вертикальным или горизонтальным отрезком (рис 2).

После определения точек пересечения возникает вопрос: какой из прямоугольников закрашивать? Это определяется исходя из направления обхода границы топологии. Заметим, что кусочно-линейная граница топологии предварительно ориентирована. Двигаясь по направлению обхода границы, справа будет находиться область, которую необходимо покрыть. Направление обхода обозначено на рисунке стрелкой, а часть квадрата, которую необходимо покрыть, обозначена наклонной штриховкой. Далее мы будем придерживаться этого обозначения.

Более сложным является пересечение квадрата с наклонным отрезком. Рассмотрим случай, когда отрезок отсекает угол квадрата (рис. 3).

В этом случае при ориентации границы топологии, как это показано на рисунке, необходимо покрыть треугольник. Алгоритм покрытия треугольника был рассмотрен ранее.

Если ориентацию изменить на противоположную (рис. 4), квадрат разбивается на треугольник и два прямоугольника.

Для первого квадрата это треугольник BCD и прямоугольники ABFE и CDGF. Аналогично и для других.

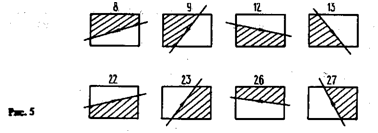
Возможен вариант, когда отрезок пересекает противоположные стороны квадрата (рис 5). В этом случае квадрат разбивается на треугольник и один прямоугольник.

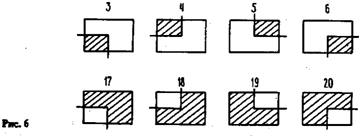
Еще одну группу стандартных ситуаций образуют пересечения границы топологии двумя отрезками, горизонтальным и вертикальным (рис. 6).

В этом случае, как видно из рис. 6, покрытие осуществляется, в зависимости от ориентации, одним или двумя прямоугольниками.

Рассмотренные стандартные ситуации являются базовыми. Однако если отношение площади лэйаута, которую необходимо покрыть, к длине границы топологии невелико или граница топологии представляет собой ломаную линию, состоящую из отрезков малой длины, уменьшения числа прямоугольников не происходит. Это объясняется тем, что стандартная ситуация возникает при приближении размера квадрата к величине минимальной экспозиции. Для устранения этого недостатка нами были разработаны новые стандартные ситуации, представляющие собой объединение базовых стандартных ситуаций. Номер стандартной ситуации получается путем слияния номеров базовых стандартных ситуаций. Легко заметить, что возможно большое число объединений со стандартными ситуациями под номерами 1,2,15,16 (рис. 7).

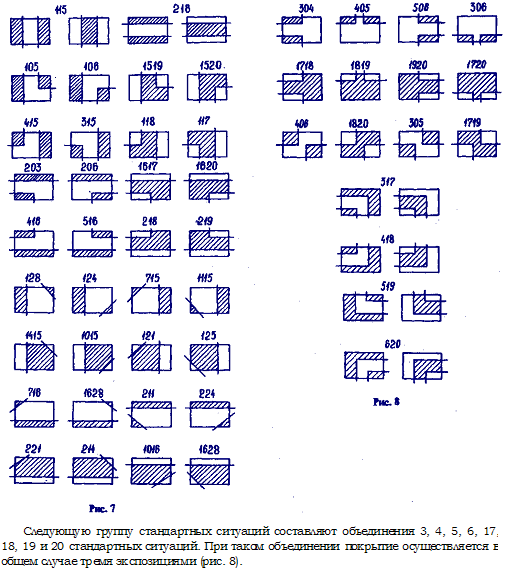
Следующую группу стандартных ситуаций составляют объединения 3, 4, 5, 6, 17, 18, 19 и 20 стандартных ситуаций. При таком объединении покрытие осуществляется в общем случае тремя экспозициями (рис. 8).

ЛИТЕРАТУРА

1. Ватанабэ М., Асада К.,Каии К., Оцуки Т. Проектирование СБИС. М.: Мир. 1988.

2. У льм ан Дж. Д. Вычислительные аспекты СБИС. М.: Радио и связь, 1990.

3. Исаков Н. М. Дифференциальные свойства негладких функций. М.: МАТИ им. К. Э. Циолковского, 1989.

4. Красносельский М. А. и др. Векторные поля на плоскости. М.: ГИФМЛ, 1963.

5. Фейнберг В. 3. Геометрические задачи машинной графики больших интегральных схем. М.: Радио и связь, 1987.

6. Мальгранж Б. Идеалы дифференцируемых функций. М.: Мир. 1968.

7. Ниренберг Л. Лекции по нелийному функциональному анализу. М.: Мир, 1977.