Обеспечение достоверности данных
Белявский Г.И., Корабельников Г.Я., Корабельникова Л.Н., Ровицкий А.К.

Предложена методика защиты данных от искажений, основанная на разработке самоконтролируемых информационных систем при ограниченном доступе (или его полном отсутствии) к их внутренним элементам.

Под достоверностью данных понимается, как правило, их свойство не иметь скрытых ошибок. В достоверности можно выделить две составляющие [ 1 ]: безошибочность — свойство не иметь в данных скрытых случайных технических ошибок; истинность — свойство не иметь в данных искажений, внесенных человеком намеренно (в том числе и из-за непонимания).

Рассмотрим один из возможных методов разработки средств для обеспечения достоверности данных, которыми должны быть оснащены вычислительные системы, реализующие сложные алгоритмы обработки данных.

Дублирование структур является одним из самых эффективных методов обеспечения достоверности данных. Если имеются достаточные для реализации дублированной информационной системы ресурсы, то это самое лучшее решение проблемы. Если ресурсов недостаточно, то, на наш взгляд, решение может быть найдено на основе методов, использующих контролирующие коды [2] и контрольные уравнения [3]. Методы, использующие контрольные уравнения, заменяют дублирующую информационную систему системой, реализующей не все структуры исходной информационной системы, а только некоторую производную от этих структур функцию.

В общем виде это выглядит следующим образом. Если U и У — входные и выходные данные информационной системы, связанной между собой Y=F (U); α и β — входные данные контролирующей системы, причем β=f(α), а также β= L(Y) (контрольное уравнение) и α=W(U), то отображения F, f, L и W удовлетворяют соотношению: L°F=f°W. Контрольное уравнение выбирают так, чтобы система была «чувствительна» к определенному заранее множеству ошибок [4], а отображения f и W должны удовлетворять данному соотношению. Если имеется несколько вариантов решений, то можно выбрать оптимальный, исходя из определенного критерия.

Рассмотрим реализацию этого подхода на примере синтеза контролирующей системы для информационной управляющей системы, функционирование которой описывается в пространстве состояний уравнениями

X(t+1)=AX(t)+ BU(t), (1)

Y(t)=CX(t),

где U (t), X (t). У (t) — векторы входа, внутреннего состояния и выхода соответственно; В, С, А — матрицы входов, выходов и внутренних состояний соответственно. Предполагается, что система (1) имеет нулевые начальные условия.

Диапазон применения подобных систем — от управления прокатным станом до управления полетом. Кроме того, такие системы присутствуют во многих информационно-измерительных системах как средство обработки сигналов (фильтры Калмана).

Рассмотрим построение контрольного уравнения, которое должно решаться в устройстве контроля. Исключим в системе (1) вектор состояний, тогда выходной вектор системы (1) в момент времени t равен

Y(t)= (2)

Соотношение (2) связывает вход с выходом. Составим скалярное произведение векторов l и У(t)

(3)

где l — некоторый вектор, определяющий контрольное соотношение. Вектор l выбирается из условия, чтобы система контроля реагировала на любой из допустимых отказов системы обработки данных. Более подробно принципы выбора вектора l изложены в работе [4].

Вычисление непосредственно по формуле (3) сложнее, чем вычисление непосредственно по формулам (1). Напомним, что контролирующая система должна быть намного проще информационной системы. Решение проблемы сложности может быть получено следующим образом.

Обозначим через V — собственный вектор, соответствующий собственному числу μ матрицы А^т. Рассмотрим уравнение

C^Tl+Z=V. (4)

Дополним матрицу С строкой

Z = (V — С^тl)^т. (5)

Расширим вектор l на одну компоненту и положим ее равной единице. Расширенный вектор обозначим через l=(l, l)^T. Тогда с учетом этого можно сделать вывод о том, что l является решением уравнения

C^T*l =v, (6)

Где C^T=( C^TV-C^Tl) (7)

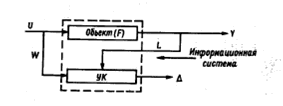
Самоконтролируемая информационная система: УК — устройство контроля; ∆ — сигнал рассогласования

Так же, как и в методе избыточных переменных [3], введем избыточную переменную r и обозначим получившийся выходной вектор через Y(t)

(8)

По динамической системе (1) с учетом уравнений (7) и (8) составим уравнения самоконтролируемой дискретной системы

(9)

Тогда контрольное уравнение, связывающее вход и выход в системе (9), будет иметь вид

(10)

где вектор W=B^T* V

Далее можно пойти двумя путями. В первом случае необходимо учесть, что в правой части уравнения (10) число слагаемых будет конечно для любого t, поскольку из условия устойчивости исходной системы (1) следует, что | μ | < 1 и, следовательно,

(11)

Недостатком контрольного уравнения (10) является необходимость запоминания последовательности (W, U(t—i)), но уравнение (10) позволяет осуществлять контроль всей системы в целом в произвольный текущий момент времени.

Другой путь состоит в добавлении к динамической системе (9) дискретной системы первого порядка

(12)

где

Таким образом, порядок системы, выполняющей функции контроля, в п раз меньше порядка исходной информации системы (1).

Если объект контроля является непрерывной динамической системой, описываемой уравнениями

(13)

то система контроля будет описываться следующим уравнением:

(14)

Как уже указывалось, полученные результаты применены для построения систем контроля информационно-управляющих и измерительных систем, связанных с обработкой больших объемов информации.

При этом сложность системы контроля практически не зависит от размерности контролируемой системы.

ЛИТЕРАТУРА

1. Дружинин Г. В. Основные проблемы обеспечения качества данных. — Межвузовский
сб. научн. тр. — М.: Изд. МИИТ, вып. 808, с. 4—6.

2. Блейхут Р. Теория и практика кодов, контролирующих ошибки. — М.: Мир, 1986. — 576 с.

3. Управление вычислительными процессами/ Под ред.' М. Б. Игнатьева. — Л.: Изд. ЛГУ, 1973. — 298 с.

4. Применение теории кодирования для коррекции искажений в линейных системах/ Г. И. Белявский, Г. Я. Корабельников, М. А. Фалькович// Изв. Сев.-Кавказ, научн. центра высш. шк. Техн. н. — Ростов н/Д, 1987, № 4.

_______________________

Г. И. Белявский - канд. техн. наук;

Г. Я- Корабельников - канд. техн. наук;

Л. Н. Корабельникова;

А. К. Ровицкий - канд. техн. наук