О журнале
Рекомендации
Об оценке надежности многократных процессов переработки данных
Соломатина А.Б.
___________________________________
Соломатина А.Б.
Рассмотрен многократный процесс переработки данных, для которого характерно многократное выполнение с некоторым сдвигом во времени одинаковых систем операций переработки данных. Предложены показатели и методы оценки надежности процессов выполнения различных функций в АСОУ.
Под надежностью процессов переработки данных (ППД) в автоматизированных системах оперативного управления (АСОУ) понимается свойство процессов своевременно обеспечивать потребителей заданным количеством данных определенного качества. При оценке надежности ППД различают одинарные процессы переработки данных — процессы выполнения отдельных задач АСОУ;
многократные ППД — процессы выполнения отдельных функций [1].
К многократным относятся процессы, для которых характерно многократное выполнение с некоторым сдвигом во времени одинаковых систем операций переработки данных в целях обеспечения систематического определенного выходного эффекта, поэтому многократное решение некоторой задачи будем рассматривать как процесс выполнения отдельной функции в АСОУ.
Показателями надежности процесса выполнения задачи являются вероятностные характеристики времени выполнения совокупности операций переработки данных, в частности, вероятность P{T3≤ tд } того, что случайное время Т3 выполнения задачи будет не больше заданного времени tд. Отказом процесса выполнения задачи считается несвоевременное его выполнение. Отказы (случаи несвоевременного выполнения) одинарных процессов решения задачи в процессе выполнения отдельной функции образуют ординарный поток отказов процесса выполнения отдельной функции. Показателями надежности процесса выполнения функции можно считать характеристики потока отказов функции, в частности, параметр ωн,з несвоевременных завершений (отказов) процессов выполнения задачи, т. е. среднее количество отказов в единицу времени.
Методы оценки надежности многократных процессов переработки данных в отличие от одинарных процессов разработаны в настоящее время недостаточно. Поэтому целесообразно получить выражение для показателя надежности процесса выполнения функции АСОУ — параметра потока несвоевременных завершений (отказов) в зависимости от показателя надежности процесса выполнения задачи G (tд)=P {T3≤ tд}.
В АСУ можно выделить два типа функций, различающихся способом Определения момента времени возникновения отказа функции. В функциях первого типа пользователю известны момент времени начала выполнения задачи и допустимое время ее выполнения или срок представления результата. В этом случае отказ функции происходит в момент времени tф функционирования системы, когда время выполнения задачи равно допустимому времени, а задача не выполнена (результаты не поступили к пользователю) (рис. 1).
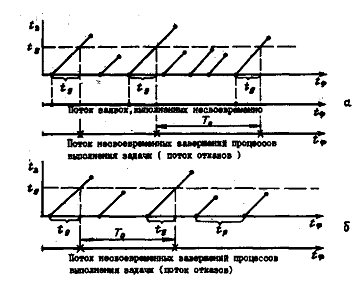
Рис. 1. Графические модели процессов выполнения функций первого типа:
а — при случайном потоке заявок на выполнение задачи; б — при регулярном потоке заявок
В функциях второго типа поступивший к пользователю результат процесса выполнения задачи содержит информацию о моменте времени начала выполнения задачи. Если время выполнения задачи превысило допустимое, то результат пользователем использован быть не может. В этом случае отказ фиксируется в момент несвоевременного завершения выполнения задачи (рис. 2).
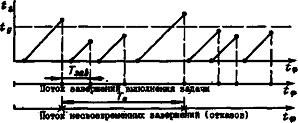
Рис. 2. Графическая модель процесса выполнения функций второго типа
В рассмотренных типах функций можно выделить функции со случайным потоком заявок на выполнение задачи и функции, в которых задачи выполняются периодически, т. е. поток заявок на выполнение задачи является регулярным.
Для стационарного режима функционирования АСУ получим выражения для ωн.з для двух типов функций при случайном и регулярном потоках заявок на выполнение задач при следующих допущениях:
продолжительности выполнения задач являются независимыми случайными величинами, распределенными по нормальному закону с математическим ожиданием М [Т3] и дисперсией D [Т3];
выполнение функций в АСОУ осуществляется назависимо друг от друга.
При стационарном режиме функционирования АСОУ поток заявок на выполнение задачи образуется в результате суперпозиции большого числа независимых, ординарных и стационарных потоков заявок от отдельных объектов управления или абонентов, что позволяет считать поток заявок на выполнение задачи простейшим.
Рассмотрим процесс выполнения отдельной функции первого типа при случайном потоке заявок на выполнение задач. Время между заявками на выполнение задач будет распределено по показательному закону с плотностью f(t)=λe-λt. Считаем, что отказ функции происходит в момент времени tф, когда t3=tД, а задача не выполнена. Тогда в потоке заявок можно выделить другой — поток несвоевременно выполненных заявок. Этот поток также является простейшим с интенсивностью λ1= λpотк, где ротк = P {T3> tД }= 1 — G (tД)=const — вероятность несвоевременного выполнения заявки. На рис. 1, а показано, что поток отказов рассматриваемой функции образуется смещением на величину tД событий простейшего потока заявок с интенсивностью λ1. Тогда среднее число отказов ωнз функции в единицу времени (параметр потока отказов) равно интенсивности λ1 потока отказов
![]()
При нормальном законе распределения времени выполнения задачи получим
![]()
где![]() — нормированная функция Лапласа.
— нормированная функция Лапласа.
Рассмотрим функцию первого типа при регулярном потоке заявок на выполнение задачи. Интервал между поступлением заявок tp = const. Время между отказами функции (рис. 1, б) является случайной величиной T0 = Ntp, где N — дискретная случайная величина. Согласно [2], время между событиями такого потока распределено по показательному закону, интенсивность которого λ2=pотк /tp .Следовательно, время между отказами функции распределено по показательному закону с математическим ожиданием М [Т0] = tp/ pотк . Тогда среднее значение параметра потока отказов функции определим как
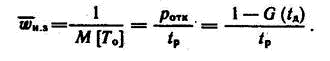
При нормальном законе распределения времени выполнения задач
получим
![]()
Рассмотрим функцию второго типа при случайном потоке заявок на выполнение задач. Считаем отказом функции несвоевременное завершение выполнения задачи. В потоке завершений выполнения задачи выделим поток несвоевременных завершений (отказов) (см. рис. 2). Получим выражение ωнз для для двух крайних случаев:
заявки на выполнение задачи являются частыми событиями;
заявки на выполнение задачи — редкие события, тогда
ωнз1 ≤ ωнз ≤ ωнз2
Процесс переработки информации при выполнении задачи можно разбить на три этапа: сбор и передача информации, обработка на ЭВМ, отображение на устройствах СОИ. Как правило, все задачи выполняются на одной ЭВМ, а время отображения результатов выполнения задач для отдельной функции практически постоянно и равно tOT=const. В первом случае, когда заявки на выполнение задачи являются частыми событиями, по окончании обработки задачи на ЭВМ сразу начинает обрабатываться следующая задача. Тогда можно считать, что время между завершениями задач распределено по закону, совпадающему с законом распределения времени обработки задачи на ЭВМ (рис. 3).
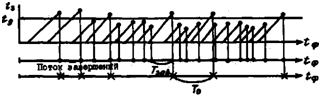
Рис. 3. Графическая модель выполнения функции второго типа при большой интенсивности потока заявок на выполнение задачи
При допущении о нормальном распределении времени обработки задачи на ЭВМ можно считать, что время между завершениями задач также распределено по нормальному закону с математическим ожиданием М [Гзав]= mt + tот и дисперсией σt2. Время То между отказами является случайной величиной, равной сумме N одинаково распределенных случайных величин Тзавi:
N
То = ![]()
i=1
где N — случайная величина, равная числу завершенных задач между отказами функции.
Поскольку закон распределения суммы нормально распределенных независимых случайных величин, среди которых нет превалирующих, — нормальный, то для определения закона распределения времени между отказами определим параметры М [Т0], D [Т0] при случайном числе слагаемых.
Рассмотрим полную группу несовместных гипотез, каждая из гипотез заключается в том, что Л' равно соответственно единице, двум, трем и т. д.
Введем гипотезы и вероятности этих гипотез:
H1:N=1 P(H1)= 1 – G(TД)= pотк,
H2:N=2 P(H2)=G(tД) [1 - G(tД)],
H3:N=3 P=(H3)=G(tД) G(tД) [1 - G(tД)] ,
Hn:N=n P(Hn)=[G(tД) n-1 [1 - G(tД)] .
Математическое ожидание при каждой гипотезе принимает значения m1=m, m2=2m, …, mn= nm, ... с вероятностями, равными вероятностям гипотез.
Применив формулу для математического ожидания дискретной случайной величины и проведя преобразования, получим
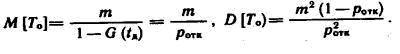
Таким образом, при нормальном распределении времени между отказами потока отказов можно определить согласно работе [1]:
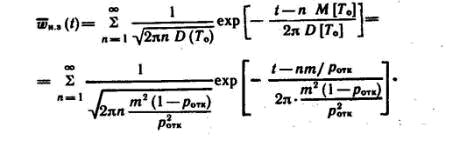
Тогда установившееся значение параметра потока отказов
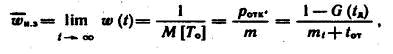
где pотк — вероятность несвоевременного завершения задачи, m=mt + tот, где mt — математическое ожидание времени обработки задачи на ЭВМ, a tот — время отображения информации на устройствах СОИ.
Рассмотрим второй случай, когда заявки на выполнение задачи являются редкими событиями (рис. 4). Случайная величина Тзав — время между

завершениями процессов выполнения отдельных задач может быть определена через следующие случайные величины:
Tзав= Т +Tзi+1 - Tзi=T + T’,
где Т— время между поступлением заявок на выполнение задачи, распределенное по показательному закону с плотностью f(t)= λe-λt;Т' = Т зi+1- Tзi , где Tзi, Т зi+1 -- времена выполнения процессов переработки данных при поступлении i-й заявки на выполнение задачи и (i +1)-й заявки соответственно.
Так как Tзi, Т зi+1 распределены нормально с параметрами М [Т3] и D [Т3], то случайная величина Т' = T3i.1 — T3i также распределена нормально с математическим ожиданием М[Т']=0 и D [T']=2D [Т3]=2σ2. Поскольку время Tо между отказами функции является случайной величиной, равной сумме случайного числа N случайных одинаково распределенных величин Тзав., то практически представляется возможным определить лишь числовые характеристики распределения времени между отказами функции.
Определим математическое ожидание и дисперсию случайной величины
Тзав:
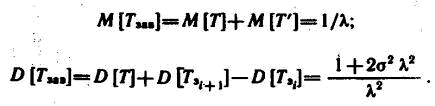
Определим числовые характеристики случайной величины Го как суммы случайного числа одинаково распределенных случайных величин Гза»:
![]()
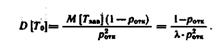
Тогда установившееся значение параметра потока отказов определяется следующим образом:
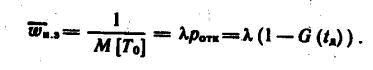
Таким образом, истинное значение параметра потока отказов для второго типа функций при случайном потоке заявок на выполнение задачи находится в интервале
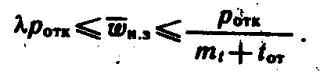
Тогда установившееся значение параметра потока отказов определяется следующим образом:
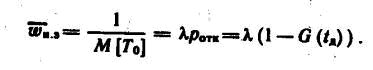
Таким образом, истинное значение параметра потока отказов для второго типа функций при случайном потоке заявок на выполнение задачи находится в интервале
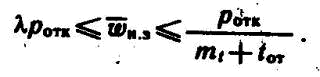
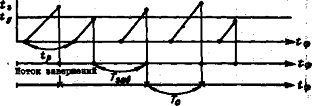
Рис. 5. Графическая модель процесса выполнения функции
второго типа при регулярном потоке заявок
На рис. 5 изображен процесс выполнения функции второго типа при регулярном потоке заявок на выполнение задачи. Случайная величина Тзав — время между завершениями процессов выполнения отдельных задач — может быть определена следующим образом: Tзав= tp +Tзi+1 - Tзi,
где tp = = const — интервал времени между поступлением заявок на выполнение задач рассматриваемой функции; Tзi, Tзi+1 — случайные величины; соответствующие времени выполнения процессов переработки данных при поступлении i-й заявки на выполнение задачи и (i + 1)-й заявки соответственно. Случайная величина Tзав распределена нормально с параметрами M[Tзав]= tp и дисперсией D [Tзав]=2D [Т3] как сумма двух нормально распределенных случайных величин. Время Tо между отказами является случайной величиной, которая определяется как сумма N нормально распределенных случайных величин Tзав . N — дискретная случайная величина, равная количеству завершений процессов выполнения задачи между отказами функции. Поэтому время Tо также является нормально распределенной случайной величиной с параметрами
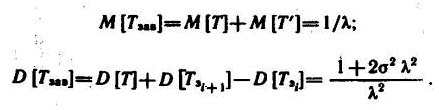
Тогда установившееся значение параметра потоке отказов определяется как
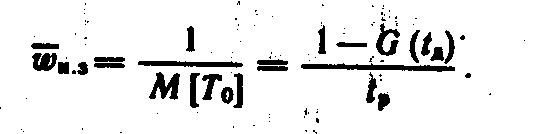
Полученные результаты могут быть использованы для оценки надёжности процессов выполнения различных функций в АСОУ.
ЛИТЕРАТУРА
1. Дружинин Г. В. Надежность автоматизированных производственных систем. — М.: Энергоатомиэдат, 1986. — 480 с.
2. К о к с Д. Р., С м и т В. Л. Теория восстановления. — М.: Сов. радио, 1967. — 299 с. 1